実践例:スタックベースの電卓
この記事では、シンプルなスタックベース(「逆ポーランド記法」スタイルとも呼ばれる)の電卓を作ります。ほぼ全て関数で実装し、特殊な型を1つ使うだけで、パターンマッチングは全く使いません。そのため、このシリーズで紹介した概念を試すのに最適な題材です。
スタックベースの電卓に慣れていない方のために説明すると、数値はスタックにプッシュされ、加算や乗算などの演算はスタックから数値をポップして結果をスタックに戻します。
以下は、スタックを使った簡単な計算を示す図です。
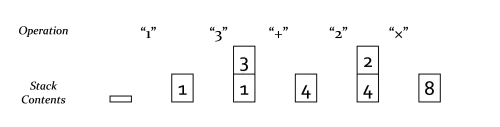
このようなシステムを設計する最初の一歩は、どう使うかを考えることです。Forthのような構文に従って、各アクションにラベルを付けます。すると、上の例は次のように記述できます。
EMPTY ONE THREE ADD TWO MUL SHOWこの構文を正確には実現できないかもしれませんが、できるだけ近づけてみましょう。
スタックのデータ型
Section titled “スタックのデータ型”まず、スタックのデータ構造を定義する必要があります。単純にするために、floatのリストを使います。
type Stack = float listしかし、もう少しわかりやすくするために、単一ケースのユニオン型でラップしましょう。
type Stack = StackContents of float listなぜこっちの方がいいのかについては、この記事で単一ケースのユニオン型について説明しています。
これで、新しいスタックを作るには StackContents をコンストラクタとして使います。
let newStack = StackContents [1.0;2.0;3.0]そして、既存のスタックの中身を取り出すには、 StackContents でパターンマッチングをします。
let (StackContents contents) = newStack
// "contents"の値は// float list = [1.0; 2.0; 3.0]プッシュ関数
Section titled “プッシュ関数”次に、スタックに数字をプッシュする方法が要ります。これは単に「 :: 」演算子を使って新しい値をリストの先頭に追加するだけです。
以下がプッシュ関数です。
let push x aStack = let (StackContents contents) = aStack let newContents = x::contents StackContents newContentsこのシンプルな関数にも、いくつか話すべきポイントがあります。
まず、リスト構造は変更できないので、関数は既存のスタックを受け取り、新しいスタックを返す必要があります。既存のスタックを変えることはできません。実は、この例のすべての関数は次のような同じ形になります。
入力:Stackと他のパラメータ出力:新しいStack次に、パラメータの順番はどうすべきでしょうか?スタックパラメータを最初にすべきか、最後にすべきか?部分適用のための関数設計の話を覚えていれば、最も変わりやすいものを最後にすべきだと思い出すでしょう。この指針が正しいことがすぐにわかります。
最後に、関数の中で let を使うのではなく、関数パラメータ自体でパターンマッチングをすると、関数をもっと簡潔にできます。
以下が書き直したバージョンです。
let push x (StackContents contents) = StackContents (x::contents)ずっと良くなりました!
ちなみに、この関数の素晴らしいシグネチャを見てください。
val push : float -> Stack -> Stack以前の記事で学んだように、シグネチャは関数について多くのことを教えてくれます。 この場合、関数の名前が “push” だと知らなくても、シグネチャだけからその機能をほぼ推測できるでしょう。 これは、わかりやすい型名を持つことがいいアイデアである理由の一つです。スタック型が単なるfloatのリストだった場合、これほど分かりやすくはなかったでしょう。
では、試してみましょう。
let emptyStack = StackContents []let stackWith1 = push 1.0 emptyStacklet stackWith2 = push 2.0 stackWith1うまく動いています!
“push”の上に組み立てる
Section titled ““push”の上に組み立てる”このシンプルな関数を用意することで、特定の数値をスタックにプッシュする操作を簡単に定義できます。
let ONE stack = push 1.0 stacklet TWO stack = push 2.0 stackしかし、よく見ると、stack パラメータが両方の操作で繰り返し使われていますね。実は、このパラメータを明示的に書く必要はありません。代わりに、部分適用を用いることで、以下のように記述できます。
let ONE = push 1.0let TWO = push 2.0let THREE = push 3.0let FOUR = push 4.0let FIVE = push 5.0これで、 push のパラメータの順番が違っていたら、こうはできなかったことがわかります。
ついでに、空のスタックを作る関数も定義しましょう。
let EMPTY = StackContents []では、これらを全部試してみましょう。
let stackWith1 = ONE EMPTYlet stackWith2 = TWO stackWith1let stackWith3 = THREE stackWith2これらの途中のスタックは邪魔ですね。取り除けないでしょうか?はい、できます!ONE、TWO、THREEなどの関数は全て同じシグネチャを持っていることに注目してください。
Stack -> Stackこれは、これらの関数をうまくつなげられるということです!一つの出力を次の入力に渡せます。こんな風に。
let result123 = EMPTY |> ONE |> TWO |> THREElet result312 = EMPTY |> THREE |> ONE |> TWOスタックからポップする
Section titled “スタックからポップする”これでスタックへのプッシュは完了しました。次は pop 関数はどうでしょう?
スタックからポップするとき、明らかにスタックの一番上を返す必要がありますが、それだけでしょうか?
オブジェクト指向スタイルでは、答えはイエスです。オブジェクト指向アプローチでは、裏でスタック自体を変更し、一番上の要素を取り除きます。
でも、関数型スタイルでは、スタックは変更できません。一番上の要素を取り除く唯一の方法は、要素が取り除かれた新しいスタックを作ることです。 呼び出し元が小さくなった新しいスタックを使えるようにするには、一番上の要素と一緒に返す必要があります。
つまり、 pop 関数は2つの値、つまり一番上と新しいスタックを返す必要があります。F#でこれを行う最も簡単な方法は、単にタプルを使うことです。
以下が実装です。
/// スタックから値を取り出し、/// その値と新しいスタックをタプルとして返すlet pop (StackContents contents) = match contents with | top::rest -> let newStack = StackContents rest (top,newStack)この関数も非常に簡単です。
前と同じように、パラメータで直接 contents を取り出しています。
次に、 match..with 式を使ってcontentsをテストします。
そして、一番上の要素を残りの部分から分け、残りの要素から新しいスタックを作り、最後にペアをタプルとして返します。
上のコードを試してみてください。コンパイルエラーが出るはずです! コンパイラは我々が見落としていたケース - スタックが空の場合はどうなるか - を見つけました。
ここで、この問題をどう処理するか決める必要があります。
- オプション1:「F# を使う理由」シリーズの記事でやったように、特別な「成功」または「エラー」状態を返す。
- オプション2:例外を投げる。
一般的に、エラーケースを使うことを好みますが、この場合は例外を使います。以下は空のケースを処理するように変えた pop コードです。
/// スタックから値を取り出し、/// その値と新しいスタックをタプルとして返すlet pop (StackContents contents) = match contents with | top::rest -> let newStack = StackContents rest (top,newStack) | [] -> failwith "Stack underflow"では、試してみましょう。
let initialStack = EMPTY |> ONE |> TWOlet popped1, poppedStack = pop initialStacklet popped2, poppedStack2 = pop poppedStackそして、アンダーフローをテストするには、
let _ = pop EMPTY数学関数を書く
Section titled “数学関数を書く”これでプッシュとポップの両方が整ったので、 add と multiply 関数に取り組めます。
let ADD stack = let x,s = pop stack // スタックの一番上を取り出す let y,s2 = pop s // 結果のスタックを取り出す let result = x + y // 計算する push result s2 // 2回取り出したスタックに戻して積む
let MUL stack = let x,s = pop stack // スタックの一番上を取り出す let y,s2 = pop s // 結果のスタックを取り出す let result = x * y // 計算する push result s2 // 2回取り出したスタックに戻して積む対話的に試してみましょう。
let add1and2 = EMPTY |> ONE |> TWO |> ADDlet add2and3 = EMPTY |> TWO |> THREE |> ADDlet mult2and3 = EMPTY |> TWO |> THREE |> MULうまく動いています!
リファクタリングの時間…
Section titled “リファクタリングの時間…”これらの2つの関数の間に大量の重複コードがあるのは明らかです。どうやってリファクタリングできるでしょうか?
両方の関数はスタックから2つの値を取り出し、何らかの二項演算を適用し、結果をスタックに戻して積みます。これにより、共通のコードを「binary」関数にリファクタリングし、二項演算関数をパラメータとして受け取るようにできます。
let binary mathFn stack = // スタックの一番上を取り出す let y,stack' = pop stack // スタックの一番上を再び取り出す let x,stack'' = pop stack' // 計算する let z = mathFn x y // 結果の値を2回取り出したスタックに積む push z stack''注意:この実装では、数字のサフィックスではなく、アポストロフィを使って「同じ」オブジェクトの変更状態を表現しています。数字のサフィックスは混乱を招きやすいためです。
ここで問題です:なぜパラメータはこの順番になっているのでしょうか? mathFn が stack の後ではなく前にあるのはなぜですか?
さて、これで binary ができたので、ADDなどをもっとシンプルに定義できます。
新しい binary ヘルパーを使ったADDの最初の試みはこんな感じです。
let ADD aStack = binary (fun x y -> x + y) aStackでも、ラムダは省略できます。これは組み込みの + 関数の定義そのものです!つまり、
let ADD aStack = binary (+) aStackそして再び、部分適用を使ってスタックパラメータを隠せます。これが最終的な定義です。
let ADD = binary (+)そして、他の数学関数の定義はこんな感じになります。
let SUB = binary (-)let MUL = binary (*)let DIV = binary (/)もう一度対話的に試してみましょう。
let div2by3 = EMPTY |> THREE|> TWO |> DIVlet sub2from5 = EMPTY |> TWO |> FIVE |> SUBlet add1and2thenSub3 = EMPTY |> ONE |> TWO |> ADD |> THREE |> SUB同じように、単項関数用のヘルパー関数も作れます。
let unary f stack = let x,stack' = pop stack // スタックの一番上を取り出す push (f x) stack' // 関数の結果をスタックに積むそして、いくつかの単項関数を定義します。
let NEG = unary (fun x -> -x)let SQUARE = unary (fun x -> x * x)再び対話的に試してみましょう。
let neg3 = EMPTY |> THREE|> NEGlet square2 = EMPTY |> TWO |> SQUAREすべてを組み合わせる
Section titled “すべてを組み合わせる”最初の要件では、結果を表示できるようにすると言いました。そこで、SHOW関数を定義しましょう。
let SHOW stack = let x,_ = pop stack printfn "答えは %f です" x stack // 同じスタックで続けるこの場合、元のスタックから取り出しますが、小さくなったスタックは無視します。関数の最終結果は元のスタックです。そうすれば、取り出されなかったかのようになります。
これで、ようやく元の要件のコード例を書くことができます。
EMPTY |> ONE |> THREE |> ADD |> TWO |> MUL |> SHOWさらに進める
Section titled “さらに進める”これは楽しいですね - 他に何ができるでしょうか?
いくつかのコアヘルパー関数を定義できます。
/// スタックの一番上の値を複製するlet DUP stack = // スタックの一番上を取得 let x,_ = pop stack // それをスタックに再度積む push x stack
/// 上位2つの値を交換するlet SWAP stack = let x,s = pop stack let y,s' = pop s push y (push x s')
/// はっきりした開始点を作るlet START = EMPTYこれらの追加関数を使うと、素敵な例をいくつか書けます。
START |> ONE |> TWO |> SHOW
START |> ONE |> TWO |> ADD |> SHOW |> THREE |> ADD |> SHOW
START |> THREE |> DUP |> DUP |> MUL |> MUL // 27
START |> ONE |> TWO |> ADD |> SHOW // 3 |> THREE |> MUL |> SHOW // 9 |> TWO |> SWAP |> DIV |> SHOW // 9 ÷ 2 = 4.5関数合成を使ってパイプを置き換える
Section titled “関数合成を使ってパイプを置き換える”でも、それだけではありません。実は、これらの関数について考える別のとても面白い方法があります。
前に言ったように、これらは全て同じシグネチャを持っています。
Stack -> Stackつまり、入力と出力の型が同じなので、これらの関数はパイプでつなぐだけでなく、合成演算子 >> を使って合成できます。
例をいくつか見てみましょう。
// 新しい関数を定義let ONE_TWO_ADD = ONE >> TWO >> ADD
// テストSTART |> ONE_TWO_ADD |> SHOW
// 新しい関数を定義let SQUARE = DUP >> MUL
// テストSTART |> TWO |> SQUARE |> SHOW
// 新しい関数を定義let CUBE = DUP >> DUP >> MUL >> MUL
// テストSTART |> THREE |> CUBE |> SHOW
// 新しい関数を定義let SUM_NUMBERS_UPTO = DUP // n >> ONE >> ADD // n+1 >> MUL // n(n+1) >> TWO >> SWAP >> DIV // n(n+1) / 2
// テストSTART |> THREE |> SQUARE |> SUM_NUMBERS_UPTO |> SHOWこれらの各ケースで、他の関数を組み合わせて新しい関数を定義しています。これは関数を組み立てる「コンビネータ」アプローチの良い例です。
パイプ vs 関数合成
Section titled “パイプ vs 関数合成”このスタックベースのモデルを使う方法を2つ見てきました。パイプを使う方法と関数合成を使う方法です。では、その違いは何でしょうか?そして、どちらの方法を好むべきでしょうか?
違いは、パイプがある意味で「リアルタイム変換」操作だということです。パイプを使うと、実際にその場で操作を行い、特定のスタックを渡します。
一方、関数合成は、やりたいことの「計画」のようなものです。一連の部品から全体的な関数を組み立てますが、まだ実際には実行しません。
たとえば、小さな操作を組み合わせて数字を2乗する「計画」を作れます。
let COMPOSED_SQUARE = DUP >> MULパイプアプローチでは同じことはできません。
let PIPED_SQUARE = DUP |> MULこれはコンパイルエラーを起こします。動かすには、何らかの具体的なスタックインスタンスが必要です。
let stackWith2 = EMPTY |> TWOlet twoSquared = stackWith2 |> DUP |> MULそしてその場合でも、COMPOSED_SQUAREの例のようにどんな入力にも対応できる計画ではなく、特定の入力に対する答えしか得られません。
「計画」を作るもう一つの方法は、始めの方で見たように、より原始的な関数にラムダを明示的に渡すことです。
let LAMBDA_SQUARE = unary (fun x -> x * x)これははるかに明示的(そしておそらく速い)ですが、関数合成アプローチのすべての利点と分かりやすさを失います。
だから、一般的には、できるだけ関数合成アプローチを選びましょう!
完全なコード
Section titled “完全なコード”これまでの例のすべてのコードを以下に示します。
// ==============================================// 型// ==============================================
type Stack = StackContents of float list
// ==============================================// スタックのプリミティブ// ==============================================
/// スタックに値を積むlet push x (StackContents contents) = StackContents (x::contents)
/// スタックから値を取り出し、/// その値と新しいスタックをタプルとして返すlet pop (StackContents contents) = match contents with | top::rest -> let newStack = StackContents rest (top,newStack) | [] -> failwith "Stack underflow"
// ==============================================// 演算子のコア// ==============================================
// 上位2つの要素を取り出す// それらに対して二項演算を行う// 結果を積むlet binary mathFn stack = let y,stack' = pop stack let x,stack'' = pop stack' let z = mathFn x y push z stack''
// 一番上の要素を取り出す// それに対して単項演算を行う// 結果を積むlet unary f stack = let x,stack' = pop stack push (f x) stack'
// ==============================================// その他のコア// ==============================================
/// スタックの一番上の値を取り出して表示let SHOW stack = let x,_ = pop stack printfn "答えは %f です" x stack // 同じスタックで続ける
/// スタックの一番上の値を複製let DUP stack = let x,s = pop stack push x (push x s)
/// 上位2つの値を交換let SWAP stack = let x,s = pop stack let y,s' = pop s push y (push x s')
/// スタックの一番上の値を削除let DROP stack = let _,s = pop stack // スタックの一番上を取り出す s // 残りを返す
// ==============================================// プリミティブに基づく単語// ==============================================
// 定数// -------------------------------let EMPTY = StackContents []let START = EMPTY
// 数字// -------------------------------let ONE = push 1.0let TWO = push 2.0let THREE = push 3.0let FOUR = push 4.0let FIVE = push 5.0
// 数学関数// -------------------------------let ADD = binary (+)let SUB = binary (-)let MUL = binary (*)let DIV = binary (/)
let NEG = unary (fun x -> -x)
// ==============================================// 関数合成に基づく単語// ==============================================
let SQUARE = DUP >> MUL
let CUBE = DUP >> DUP >> MUL >> MUL
let SUM_NUMBERS_UPTO = DUP // n >> ONE >> ADD // n+1 >> MUL // n(n+1) >> TWO >> SWAP >> DIV // n(n+1) / 2これで、シンプルなスタックベースの電卓ができました。いくつかの基本的な操作( push 、 pop 、 binary 、 unary )から始めて、実装も使用も簡単な、完全なドメイン固有言語を組み立てられることがわかりました。
気づいたかもしれませんが、この例はForth言語に大きく基づいています。無料の本「Thinking Forth」を強くお勧めします。これはForth言語だけでなく、(オブジェクト指向ではない)問題分解技術についての本で、関数型プログラミングにも同じように当てはまる内容です。
この記事のアイデアは、Ashley Fenielloの素晴らしいブログから得ました。F#でスタックベース言語をエミュレートすることについてもっと深く学びたい場合は、そこから始めてください。楽しんでください!