この投稿は、シリーズの2番目です。 前回の投稿では、通常の世界から高次の世界へ値を持ち上げるためのコア関数について説明しました。

今回は、「世界をまたぐ」関数と、bind関数を使ってそれらを制御する方法を見ていきます。

シリーズの内容

このシリーズで言及する様々な関数へのショートカットリストです。

パート2：世界をまたぐ関数の合成方法

bind関数

一般的な名前：bind、flatMap、andThen、collect、SelectMany

一般的な演算子：>>=（左から右）、=<<（右から左）

機能：世界をまたぐ（「モナディックな」）関数の合成

シグネチャ：(a->E<b>) -> E<a> -> E<b>、または引数を逆にして：E<a> -> (a->E<b>) -> E<b>

説明

通常の世界と高次の世界を行き来する関数をよく扱います。

たとえば、stringをintに解析する関数が通常のintではなくOption<int>を返したり、 ファイルから行を読み込む関数がIEnumerable<string>を返したり、 Webページを取得する関数がAsync<string>を返したりします。

このような「世界をまたぐ」関数は、a -> E<b>というシグネチャで認識できます。入力は通常の世界にありますが、出力は高次の世界にあります。 残念ながら、このタイプの関数は標準的な合成では連結できません。

「bind」の機能は、世界をまたぐ関数（一般に「モナディック関数」と呼ばれる）を持ち上げられた関数E<a> -> E<b>に変換することです。

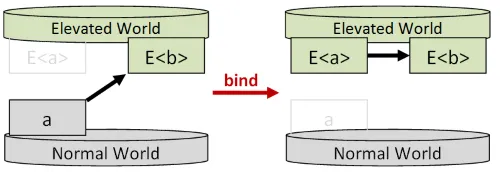
これを行う利点は、結果として得られる持ち上げられた関数が純粋に高次の世界に存在し、簡単に合成できることです。

たとえば、a -> E<b>型の関数はb -> E<c>型の関数と直接合成できませんが、 bindを使用すると、2番目の関数はE<b> -> E<c>型になり、合成可能になります。

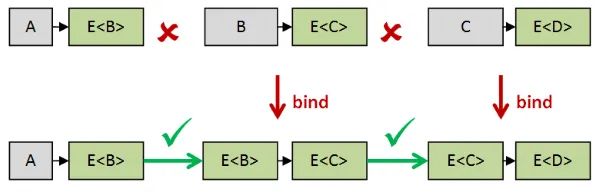
このように、bindを使えば任意の数のモナディック関数を連鎖できます。

別の解釈

bindの別の捉え方として、高次の値（E<a>）とモナディック関数（a -> E<b>）という2つの引数を取り、 入力の中身を「アンラップ」してa -> E<b>関数を実行することで新しい高次の値（E<b>）を生成する関数と考えられます。 この「アンラップ」という比喩はすべての高次の世界に当てはまるわけではありませんが、こう考えると役立つことが多いです。

実装例

F#で2つの型に対してbindを定義した例を見てみましょう。

module Option = 

    // オプション用のbind関数
    let bind f xOpt = 
        match xOpt with
        | Some x -> f x
        | _ -> None
    // 型：('a -> 'b option) -> 'a option -> 'b option

module List = 

    // リスト用のbind関数
    let bindList (f: 'a->'b list) (xList: 'a list)  = 
        [ for x in xList do 
          for y in f x do 
              yield y ]
    // 型：('a -> 'b list) -> 'a list -> 'b list

注意：

  • この2つの場合、F#ではすでにOption.bindとList.collectとして関数が存在します。
  • List.bindでは再びfor..in..doを使っていますが、この実装がリストでのbindの動きを明確に示しています。 純粋な再帰的実装もありますが、ここでは省略します。

使用例

冒頭で述べたように、bindは世界をまたぐ関数を合成するのに使えます。 シンプルな例でその動きを見てみましょう。

まず、特定のstringをintに解析する関数があるとします。とてもシンプルな実装です。

let parseInt str = 
    match str with
    | "-1" -> Some -1
    | "0" -> Some 0
    | "1" -> Some 1
    | "2" -> Some 2
    // 以下同様
    | _ -> None

// シグネチャはstring -> int option

時には整数を返し、時には返しません。そのため、シグネチャはstring -> int optionとなり、世界をまたぐ関数です。

そして、intを入力として受け取り、OrderQty型を返す別の関数があるとします。

type OrderQty = OrderQty of int

let toOrderQty qty = 
    if qty >= 1 then 
        Some (OrderQty qty)
    else
        // 正の数のみ許可
        None

// シグネチャはint -> OrderQty option

これも、入力が正でない場合はOrderQtyを返さないかもしれません。したがって、シグネチャはint -> OrderQty optionとなり、これも世界をまたぐ関数です。

では、文字列を直接OrderQtyに変換する関数をどのように作れば良いでしょうか。

parseIntの出力を直接toOrderQtyに渡せないので、ここでbindが役立ちます。

Option.bind toOrderQtyを実行すると、int option -> OrderQty option関数に持ち上げられ、parseIntの出力を入力として使えます。

let parseOrderQty str =
    parseInt str
    |> Option.bind toOrderQty
// シグネチャはstring -> OrderQty option

新しいparseOrderQty関数のシグネチャはstring -> OrderQty optionとなり、これもまた世界をまたぐ関数です。 そのため、出力のOrderQtyを使って何かをする場合は、チェーンの次の関数でもbindを使う必要があるかもしれません。

中置演算子版のbind

applyと同様に、名前付きのbind関数は扱いづらいことがあります。そのため、中置演算子版を作るのが一般的です。 通常、左から右へのデータの流れには>>=、右から左への流れには=<<を使います。

これを使えば、parseOrderQtyの別バージョンを次のように書けます。

let parseOrderQty_alt str =
    str |> parseInt >>= toOrderQty

ご覧の通り、>>=はパイプ演算子（|>）と同じような役割を果たしますが、「高次の」値を世界をまたぐ関数にパイプするのに使います。

「プログラム可能なセミコロン」としてのbind

bindは任意の数の関数や式を連鎖させるのに使えるので、次のようなコードがよく見られます。

expression1 >>= 
expression2 >>= 
expression3 >>= 
expression4

これは、命令型プログラムで>>=をセミコロン（;）に置き換えたものとさほど変わりません。

statement1; 
statement2;
statement3;
statement4;

このため、bindは「プログラム可能なセミコロン」と呼ばれることがあります。

bindとreturnの言語サポート

ほとんどの関数型プログラミング言語には、bindのための何らかの構文サポートがあり、一連の継続を書いたり、明示的にbindを使ったりしなくて済むようになっています。

F#では、これはコンピュテーション式の（一つの）要素です。次のような明示的なbindの連鎖は次のように書けます。

initialExpression >>= (fun x ->
expressionUsingX  >>= (fun y ->
expressionUsingY  >>= (fun z ->
x+y+z )))             // return

これをlet!構文を使って暗黙的に表現できます。

elevated {
    let! x = initialExpression 
    let! y = expressionUsingX x
    let! z = expressionUsingY y
    return x+y+z }

Haskellでは、同等のものは「do記法」と呼ばれます。

do
    x <- initialExpression 
    y <- expressionUsingX x
    z <- expressionUsingY y
    return x+y+z

Scalaでは、同等のものは「for内包表記」と呼ばれます。

for {
    x <- initialExpression 
    y <- expressionUsingX(x)
    z <- expressionUsingY(y)
} yield {    
    x+y+z
}

bind/returnを使う際に特別な構文を使う必要はないことを強調しておくのは重要です。他の関数と同じように、bindや>>=を常に使えます。

Bind vs. Apply vs. Map

bindとreturnの組み合わせは、applyとreturnよりもさらに強力だと考えられています。 なぜなら、bindとreturnがあればmapとapplyを構築できますが、その逆はできないからです。

たとえば、bindを使ってmapをエミュレートする方法を見てみましょう。

  • まず、通常の関数から世界をまたぐ関数を構築します。出力にreturnを適用することでこれを行います。
  • 次に、この世界をまたぐ関数をbindを使って持ち上げられた関数に変換します。これにより、単にmapを行った場合と同じ結果が得られます。

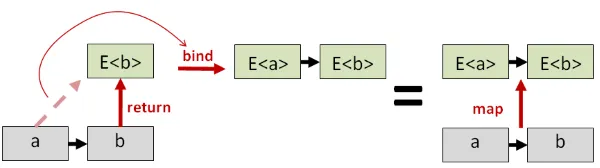
同様に、bindはapplyをエミュレートできます。以下は、F#でOptionに対するmapとapplyをbindとreturn（Some）を使って定義する方法です。

// bindとreturn (Some)を使ってmapを定義
let map f = 
    Option.bind (f >> Some) 

// bindとreturn (Some)を使ってapplyを定義
let apply fOpt xOpt = 
    fOpt |> Option.bind (fun f -> 
        let map = Option.bind (f >> Some)
        map xOpt)

この時点で、人々はしばしば「bindがより強力なのに、なぜapplyを使うべきなのか」と疑問に思います。

答えは、applyがbindでエミュレートできるからといって、そうすべきだというわけではないということです。 たとえば、bindの実装ではエミュレートできない方法でapplyを実装することも可能です。

実際、apply（「アプリカティブスタイル」）やbind（「モナディックスタイル」）を使うことで、プログラムの動作に大きな影響を与える可能性があります。 これら2つのアプローチの詳細については、このポストのパート3で説明します。

正しいbind/return実装の特性

mapの場合と同様に、またapply/returnの場合と同様に、 正しいbind/returnの実装には、どの高次の世界で作業していても真となるべき特性がいくつかあります。

いわゆる3つの「モナド則」があります。 （プログラミングの観点での）モナドを定義する一つの方法は、ジェネリック型コンストラクタE<T>とモナド則に従う関数のペア（bindとreturn）から成るものと言うことです。 モナドを定義する方法はこれだけではありません。数学者は通常、少し異なる定義を使います。 しかし、ジェネリック型コンストラクタと2つの関数によるこの定義が、プログラマにとって最も役立ちます。

これまでに見たファンクターとアプリカティブの法則と同様に、これらの法則はかなり理にかなっています。

まず、return関数自体が世界をまたぐ関数であることに注目してください。

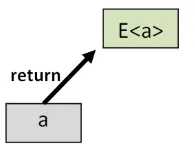
これは、bindを使ってそれを高次の世界の関数に持ち上げられることを意味します。そして、この持ち上げられた関数は何をするのでしょうか。うまくいけば、何もしません！ 単に入力を返すだけです。

そして、これがまさに最初のモナド則です。この持ち上げられた関数は、高次の世界でのid関数と同じでなければならないと言っています。

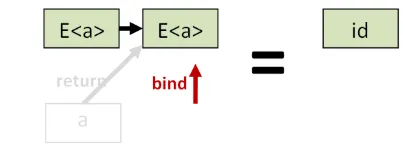
2番目の法則は似ていますが、bindとreturnが逆になっています。通常の値aと、aをE<b>に変換する世界をまたぐ関数fがあるとします。

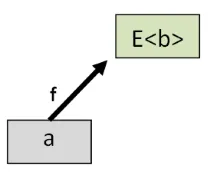
fにはbindを、aにはreturnを使って、両方を高次の世界に持ち上げましょう。

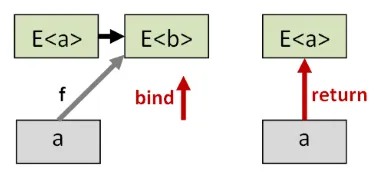
ここで、fの高次バージョンをaの高次バージョンに適用すると、ある値E<b>が得られます。

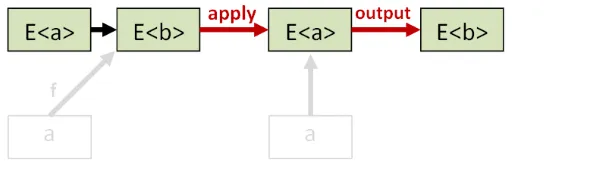
一方、fの通常バージョンをaの通常バージョンに適用しても、ある値E<b>が得られます。

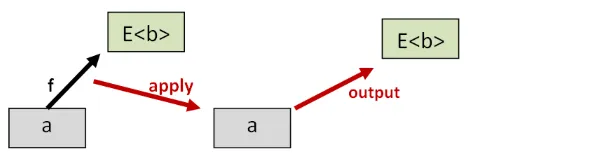
2番目のモナド則は、これら2つの高次の値（E<b>）が同じであるべきだと言っています。言い換えれば、これらの bind と return の適用はデータを歪めるべきではありません。

3番目のモナド則は結合法則に関するものです。

通常の世界では、関数合成は結合法則を満たします。 たとえば、値を関数fにパイプし、その結果を関数gにパイプすることができます。 あるいは、最初にfとgを合成して単一の関数にしてから、aをそれにパイプすることもできます。

let groupFromTheLeft = (a |> f) |> g
let groupFromTheRight = a |> (f >> g)

通常の世界では、これらの代替案が同じ答えを与えることを期待します。

3番目のモナド則は、bindとreturnを使用した後でも、グループ化は問題にならないと言っています。以下の2つの例は、上記の例に対応します。

let groupFromTheLeft = (a >>= f) >>= g
let groupFromTheRight = a >>= (fun x -> f x >>= g)

そして再び、これらの両方が同じ答えを与えることを期待します。

リストはモナドではない。オプションもモナドではない。

モナドは3つの要素から成ります。ジェネリック型（別名「型コンストラクタ」）、2つの関数、そして満たすべき一連の特性です。

したがって、Listデータ型はモナドの1つの構成要素にすぎず、Optionデータ型も同様です。ListとOptionは、それ自体ではモナドではありません。

モナドを変換として考えるのがより適切かもしれません。 「リストモナド」は通常の世界を高次の「リスト世界」に変換するものであり、「オプションモナド」は通常の世界を高次の「オプション世界」に変換するものです。

ここに多くの混乱の源があると思います。「リスト」という言葉には多くの異なる意味があります。

  1. List<int>のような具体的な型またはデータ構造。
  2. 型コンストラクタ（ジェネリック型）：List<T>。
  3. Listクラスやモジュールのような型コンストラクタと何らかの操作。
  4. 型コンストラクタと何らかの操作、そしてそれらの操作がモナド則を満たすもの。

モナドなのは最後のものだけです！他の意味も有効ですが、混乱の原因となります。

また、最後の2つのケースはコードを見ただけでは区別がつきにくいです。残念ながら、モナド則を満たしていない実装も存在します。 「モナド」と呼ばれていても、必ずしも真のモナドではない場合があるのです。

個人的に、このサイトでは「モナド」という言葉の使用を避けています。代わりに、bind関数に焦点を当てています。 抽象的な概念ではなく、問題解決のためのツールキットの一部として扱うためです。

そのため、「これはモナドですか？」とは尋ねないでください。

代わりに、次のように尋ねるべきです。使えるbindとreturn関数がありますか？そして、それらは正しく実装されていますか？

まとめ

これでコア関数が4つ揃いました。map、return、apply、そしてbindです。これらの機能がそれぞれ明確になったことを願っています。

しかし、まだ答えていない質問もあります。たとえば次のような疑問です。 「なぜapplyの代わりにbindを選ぶべきなのか？」「複数の高次の世界を同時に扱うにはどうすればよいのか？」

次の投稿では、これらの疑問に答え、一連の実践的な例を通じてこのツールセットの使い方を示します。

更新：@joseanpgに指摘されたモナド則の誤りを修正しました。ありがとうございます！

results matching ""

    No results matching ""