この連載では、OptionやListなどのジェネリックなデータ型を扱うためのコア関数を解説します。
これは、関数型パターンに関する私の講演の続編です。
このような内容を書かないと約束したのは承知していますが、 今回は少し違うアプローチを試みました。 型クラスなどの抽象概念ではなく、コア関数自体とその実践的な使用方法に焦点を当てることが有用だと考えたのです。
つまり、これはmap、return、apply、bindの一種の「マニュアルページ」のようなものです。
各関数について、名前（と一般的な別名）、よく使われる演算子、型シグネチャを紹介します。 さらに、なぜその関数が必要で、どのように使われるのかを詳しく説明します。その際、視覚的な補助も交えます（私はこれが常に役立つと感じています）。
Haskellユーザーや圏論家の方々は、ここで目をそらしたくなるかもしれません。 数学的な内容はなく、かなり大雑把な説明になります。専門用語やHaskell特有の概念（型クラスなど）は避け、できるだけ全体像に焦点を当てます。 ここで紹介する概念は、どんな言語の関数型プログラミングにも応用できるはずです。
このアプローチが好みに合わない方もいるでしょう。それで構いません。 ウェブ上にはたくさんの、より学術的な説明があります。 これやこれから始めてみるのもいいでしょう。
最後に、このサイトの多くの投稿と同じく、これも私自身の学習過程の一環として書いています。 私は決して専門家ではないので、間違いがあればぜひ指摘してください。
背景
まずは背景と用語の説明から始めましょう。
2つの世界でプログラミングできると想像してください。「通常の」日常的な世界と、「高次の世界」（この名前の理由はすぐに説明します）と呼ぶ世界です。
高次の世界は通常の世界とよく似ています。実際、通常の世界のすべてのものには、高次の世界に対応するものがあります。
たとえば、通常の世界にはIntという値の集合がありますが、高次の世界にはそれに対応するE<Int>という値の集合があります。
同様に、通常の世界のStringに対して、高次の世界にはE<String>があります。
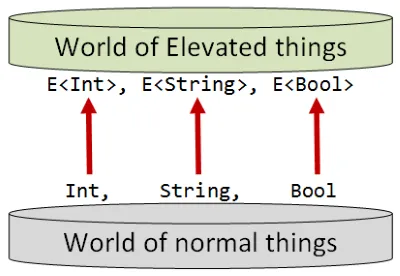
また、通常の世界にIntとStringの間の関数があるように、高次の世界にもE<Int>とE<String>の間の関数があります。
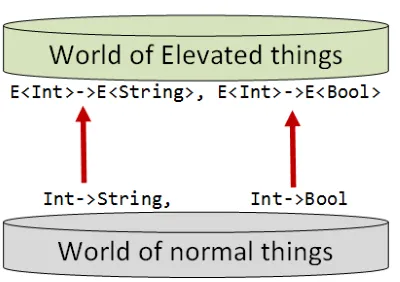
「世界」という言葉を「型」の代わりに意図的に使っていることに注意してください。世界内の値の間の関係が、基礎となるデータ型と同じくらい重要だということを強調するためです。
高次の世界とは具体的に何か？
高次の世界を正確に定義するのは難しいです。高次の世界には多くの種類があり、それらに共通点がないからです。
データ構造（Option<T>）を表すもの、ワークフロー（State<T>）を表すもの、
シグナル（Observable<T>）を表すもの、非同期値（Async<T>）を表すもの、その他の概念を表すものがあります。
様々な高次の世界に具体的な共通点はありませんが、それらを扱う方法には共通点があります。 異なる高次の世界でも同じような問題が繰り返し発生します。そして、 これらの問題に対処するための標準的なツールやパターンを使うことができます。
この連載では、これらのツールとパターンについて説明していきます。
シリーズの内容
このシリーズは以下のように展開します。
- まず、通常のものを高次の世界に持ち上げるためのツールを説明します。これには
map、return、apply、bindなどの関数が含まれます。 - 次に、高次の値を異なる方法で組み合わせる方法を見ていきます。これは値が独立しているか依存しているかによって変わってきます。
- その後、リストと他の高次の値を混ぜる方法をいくつか紹介します。
- 最後に、これらのテクニックをすべて使用する2つの実際の例を見ます。そこで偶然にもReaderモナドを発明することになります。
以下は、様々な関数へのショートカットリストです。
- パート1：高次の世界への持ち上げ
- パート2：世界をまたぐ関数の合成方法
- パート3：コア関数の実際的な使い方
- パート4：リストと高次の値の混合
- パート5：すべてのテクニックを使用する実世界の例
- パート6：独自の高次の世界を設計する
- パート7：まとめ
パート1：高次の世界への持ち上げ
最初の課題は、通常の世界から高次の世界にどうやって到達するかです。
まず、特定の高次の世界について以下を仮定します。
- 通常の世界のすべての型には、高次の世界に対応する型があります。
- 通常の世界のすべての値には、高次の世界に対応する値があります。
- 通常の世界のすべての関数には、高次の世界に対応する関数があります。
通常の世界から高次の世界に何かを移動させる概念を「持ち上げ」と呼びます。これが「高次の世界」という言葉を使った理由です。
これらの対応するものを「持ち上げられた型」「持ち上げられた値」「持ち上げられた関数」と呼びます。
各高次の世界は異なるので、持ち上げの共通の実装はありません。しかし、mapやreturnなどの様々な「持ち上げ」パターンに名前を付けることはできます。
注意：これらの持ち上げられた型に標準的な名前はありません。「ラッパー型」「拡張型」「モナド型」などと呼ばれているのを見たことがあります。 これらの名前のどれにも満足できなかったので、新しい名前を発明しました！ また、仮定を避けようとしているので、持ち上げられた型が何らかの形で優れているとか、追加情報を含んでいるとか示唆したくありません。 この投稿で「高次」という言葉を使うことで、型自体よりも持ち上げのプロセスに焦点を当てられることを願っています。
「モナディック」という言葉を使うのは正確ではありません。これらの型がモナドの一部である必要はないからです。
map関数
一般的な名前 map、fmap、lift、Select
一般的な演算子 <$>、<!>
機能 関数を高次の世界に持ち上げます
シグネチャ (a->b) -> E<a> -> E<b>。あるいはパラメータを逆にして E<a> -> (a->b) -> E<b>
説明
「map」は、通常の世界の関数を取り、高次の世界の対応する関数に変換するための一般的な名前です。
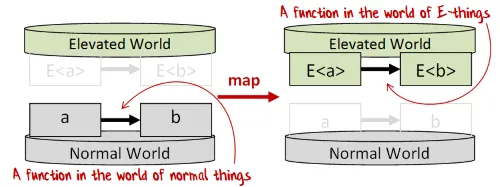
各高次の世界では、mapが独自の方法で実装されています。
別の見方
mapには別の見方もあります。高次の値（E<a>）と通常の関数（a->b）を受け取り、E<a>の内部要素に関数a->bを適用して生成された新しい高次の値（E<b>）を返す、
2つのパラメータを持つ関数と考えることもできます。
F#のように関数がデフォルトでカリー化される言語では、これらの見方は同じことを意味します。 他の言語では、2つの使い方を切り替えるために、カリー化や非カリー化が必要になることがあります。
2つのパラメータを取るバージョンでは、シグネチャがE<a> -> (a->b) -> E<b>となることが多いです。
高次の値が先で、通常の関数が後ろです。抽象的には同じことで、mapの概念は変わりません。
しかし、パラメータの順序は実際にmap関数を使う際に影響します。
実装例
F#でのオプションとリストのmap実装例を見てみましょう。
/// オプションのmap
let mapOption f opt =
match opt with
| None ->
None
| Some x ->
Some (f x)
// 型：('a -> 'b) -> 'a option -> 'b option
/// リストのmap
let rec mapList f list =
match list with
| [] ->
[]
| head::tail ->
// 新しいhead + 新しいtail
(f head) :: (mapList f tail)
// 型：('a -> 'b) -> 'a list -> 'b list
これらは実際には組み込み関数ですが、一般的な型のmapがどのようなものかを示すために実装例を挙げました。
使用例
F#でのmapの使い方をいくつか見てみましょう。
// 通常の世界で関数を定義
let add1 x = x + 1
// 型：int -> int
// オプションの世界に持ち上げた関数
let add1IfSomething = Option.map add1
// 型：int option -> int option
// リストの世界に持ち上げた関数
let add1ToEachElement = List.map add1
// 型：int list -> int list
これらのマップされた関数を使うと、次のようなコードが書けます。
Some 2 |> add1IfSomething // Some 3
[1;2;3] |> add1ToEachElement // [2; 3; 4]
多くの場合、中間的な関数を作らずに、部分適用を直接使います。
Some 2 |> Option.map add1 // Some 3
[1;2;3] |> List.map add1 // [2; 3; 4]
正しいmap実装の特徴
高次の世界は、ある意味で通常の世界を映し出しています。通常の世界の関数には、高次の世界に対応する関数があります。
mapは、この対応関係を適切に保つ必要があります。
たとえば、addのmapが誤ってmultiplyの高次版を返したり、lowercaseのmapがuppercaseの高次版を返したりしてはいけません。
では、あるmap実装が本当に正しい対応関数を返しているかを、どうやって確認できるでしょうか？
プロパティベースのテストに関する私の投稿で説明したように、関数の正しい実装は、特定の例ではなく一般的な特性を使って定義し、テストすることができます。
これはmapにも当てはまります。
実装は特定の高次の世界によって異なりますが、どの場合も、奇妙な動作を避けるために満たすべき特定の特性があります。
まず、通常の世界のid関数をmapで高次の世界に持ち上げると、
結果の関数は高次の世界のid関数と同じになるはずです。
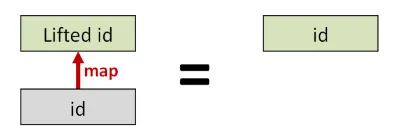
次に、通常の世界で2つの関数fとgを取り、それらを合成して（たとえばhとする）、その結果をmapで持ち上げると、
得られる関数は、fとgを別々に高次の世界に持ち上げてから合成した場合と同じになるはずです。
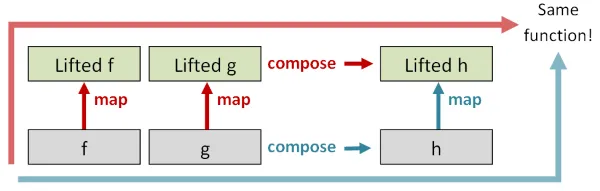
これら2つの特性は「ファンクター則」と呼ばれ、
ファンクター（プログラミングの文脈で）は、ジェネリックなデータ型（ここではE<T>）とファンクター則に従うmap関数のペアとして定義されます。
注意：「ファンクター」という言葉は混乱を招きやすいです。圏論の意味でのファンクターと、プログラミングの意味でのファンクター（上記で定義）があります。 さらに、ライブラリで定義された「ファンクター」もあります。 たとえば、HaskellのFunctor型クラスや、ScalazのFunctorトレイトです。 SMLやOCaml（そしてC++）のファンクターには触れませんが、 これらはまた別物です！
そのため、私は「マッピング可能な」世界について話すことを好みます。実際のプログラミングでは、何らかの形でマッピングできない高次の世界を見つけるのは難しいでしょう。
mapの変種
mapにはよく使われる変種がいくつかあります。
- 定数map。定数map（別名を「置換」map）は、関数の出力ではなく定数ですべての値を置き換えます。 場合によっては、このような特殊な関数を使うとより効率的な実装が可能です。
- 世界をまたぐ関数を扱うmap。map関数
a->bは完全に通常の世界に属しています。しかし、マッピングしたい関数が 通常の世界に戻らず、別の高次の世界の値を返す場合はどうでしょうか？ この課題への対処方法は後の投稿で見ていきます。
return関数
一般的な名前 return、pure、unit、yield、point
一般的な演算子 なし
機能 単一の値を高次の世界に持ち上げます
シグネチャ a -> E<a>
説明
「return」（「unit」や「pure」とも呼ばれる）は、通常の値を高次の値に変換する単純な関数です。
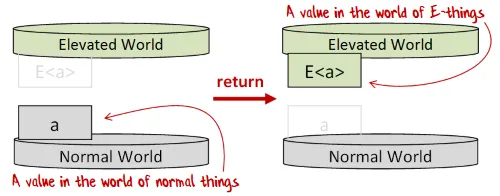
この関数には様々な名前がありますが、ここではF#で一般的に使われ、コンピュテーション式でも使用される「return」を一貫して使います。
注意：ここではpureとreturnの違いには触れません。型クラスはこの記事の主題ではないためです。
実装例
F#でのreturnの実装例を見てみましょう。
// オプションの世界に値を持ち上げる
let returnOption x = Some x
// 型：'a -> 'a option
// リストの世界に値を持ち上げる
let returnList x = [x]
// 型：'a -> 'a list
もちろん、オプションやリスト用にこのような特別な関数を定義する必要はありません。ここでは一般的な型のreturnの例として示しています。
apply関数
一般的な名前 apply、ap
一般的な演算子 <*>
機能 高次の値の中に包まれた関数を、E<a> -> E<b>という持ち上げられた関数に展開します
シグネチャ E<(a->b)> -> E<a> -> E<b>
説明
「apply」は、高次の値の中に包まれた関数（E<(a->b)>）を、E<a> -> E<b>という形の持ち上げられた関数に変換します。
一見すると重要性が分かりにくいかもしれませんが、実は非常に有用です。通常の世界の複数引数関数を高次の世界の複数引数関数に持ち上げることができるからです。 この点については後ほど詳しく見ていきます。
別の見方
applyには別の見方もあります。
高次の値（E<a>）と高次の関数（E<(a->b)>）を受け取り、関数a->bをE<a>の中身に適用して新しい高次の値（E<b>）を作る、2つの引数を持つ関数と考えることもできます。
たとえば、1引数の関数（E<(a->b)>）があれば、それを1つの高次の引数に適用して、結果を別の高次の値として得ることができます。
2引数の関数（E<(a->b->c)>）があれば、applyを2回続けて使い、2つの高次の引数を適用して高次の出力を得ることができます。
このテクニックを使えば、任意の数の引数に対応できます。
実装例
F#での2つの異なる型に対するapplyの定義例を見てみましょう。
module Option =
// オプション用のapply関数
let apply fOpt xOpt =
match fOpt,xOpt with
| Some f, Some x -> Some (f x)
| _ -> None
module List =
// リスト用のapply関数
// [f;g] apply [x;y] は [f x; f y; g x; g y] になる
let apply (fList: ('a->'b) list) (xList: 'a list) =
[ for f in fList do
for x in xList do
yield f x ]
ここでは、applyOptionやapplyListのような名前ではなく、同じ名前を使い、型ごとにモジュールに入れています。
List.applyの実装では、最初のリストの各関数が2番目のリストの各値に適用され、「直積」のような結果になります。
つまり、関数のリスト[f; g]を値のリスト[x; y]に適用すると、4要素のリスト[f x; f y; g x; g y]になります。
これが唯一の方法ではないことは後で見ていきます。
なお、この実装はfor..in..doループ（既存の機能）を使っているので、少し手抜きをしています！
これはapplyの動作を分かりやすく示すためです。「ゼロから」再帰的な実装を作るのは簡単ですが（ただし、適切な末尾再帰にするのはそれほど簡単ではありません！）、
ここでは実装よりも概念に焦点を当てたいと思います。
applyの中置演算子版
apply関数をそのまま使うのは少し不便なので、一般的に中置演算子版を作ります。通常<*>と呼ばれます。
これを使うと、次のようなコードが書けます。
let resultOption =
let (<*>) = Option.apply
(Some add) <*> (Some 2) <*> (Some 3)
// resultOption = Some 5
let resultList =
let (<*>) = List.apply
[add] <*> [1;2] <*> [10;20]
// resultList = [11; 21; 12; 22]
Apply vs. Map
applyとreturnの組み合わせはmapよりも「強力」と考えられています。
applyとreturnがあればmapを構築できますが、その逆はできないからです。
仕組みはこうです。通常の関数にreturnを適用し、その後applyを使うと、
単にmapを使った場合と同じ結果になります。
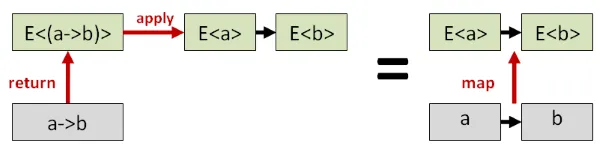
このテクニックを使うと、中置記法をさらに簡単にできます。
最初のreturnとapplyをmapで置き換えられるので、一般的にmap用の中置演算子も作ります。F#では通常<!>を使います。
let resultOption2 =
let (<!>) = Option.map
let (<*>) = Option.apply
add <!> (Some 2) <*> (Some 3)
// resultOption2 = Some 5
let resultList2 =
let (<!>) = List.map
let (<*>) = List.apply
add <!> [1;2] <*> [10;20]
// resultList2 = [11; 21; 12; 22]
このコードは、通常の関数を使う場合とよく似た見た目になります。つまり、通常のadd x yの代わりに、似たようなadd <!> x <*> yを使えます。
ただし、ここでのxとyは通常の値ではなく高次の値です。この記法を「オーバーロードされた空白」と呼ぶ人もいるほどです！
もう一つ面白い例を見てみましょう。
let batman =
let (<!>) = List.map
let (<*>) = List.apply
// +を使った文字列の連結
(+) <!> ["bam"; "kapow"; "zap"] <*> ["!"; "!!"]
// 結果 =
// ["bam!"; "bam!!"; "kapow!"; "kapow!!"; "zap!"; "zap!!"]
正しいapply/return実装の特徴
mapと同じように、applyとreturnのペアの正しい実装も、どの高次の世界で使う場合でも成り立つべき特徴があります。
いわゆる4つの「アプリカティブ則」があり、
アプリカティブファンクター（プログラミングの文脈で）は、ジェネリックなデータ型コンストラクター（我々の場合はE<T>）と、
アプリカティブ則に従う関数のペア（applyとreturn）として定義されます。
mapの法則と同様に、これらの法則もとても理にかなっています。そのうちの2つを紹介しましょう。
最初の法則は次のように言います。通常の世界のid関数を取り、returnで高次の世界に持ち上げ、それからapplyを行うと、
得られる新しい関数（E<a> -> E<a>型）は高次の世界のid関数と同じになるべきだ、と。
2番目の法則はこうです。通常の世界で関数fと値xを取り、fをxに適用して結果（たとえばy）を得て、その結果をreturnで持ち上げると、
fとxを先に高次の世界に持ち上げてから、そこで後から適用した場合と同じ結果になるべきだ、と。
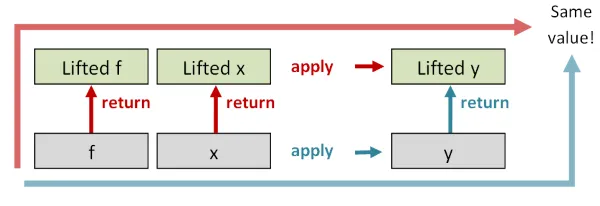
残りの2つの法則は図で表現しにくいので、ここでは説明しません。ただ、これらの法則を全て合わせることで、どんな実装も適切であることが保証されます。
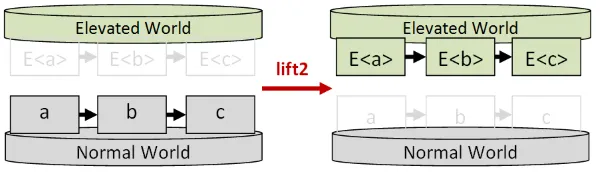
liftN関数ファミリー
一般的な名前 lift2、lift3、lift4など
一般的な演算子 なし
機能 指定された関数を使って2つ（または3つ、4つ）の高次の値を組み合わせます
シグネチャ
lift2: (a->b->c) -> E<a> -> E<b> -> E<c>
lift3: (a->b->c->d) -> E<a> -> E<b> -> E<c> -> E<d>
など
説明
applyとreturn関数を使って、liftN（lift2、lift3、lift4など、Nは2,3,4などの数）と呼ばれる一連のヘルパー関数を定義できます。
これらは、N個の引数を持つ通常の関数を取り、対応する高次の関数に変換します。
lift1は単にmapと同じなので、通常は別の関数として定義しません。
実装例を見てみましょう。
module Option =
let (<*>) = apply
let (<!>) = Option.map
let lift2 f x y =
f <!> x <*> y
let lift3 f x y z =
f <!> x <*> y <*> z
let lift4 f x y z w =
f <!> x <*> y <*> z <*> w
lift2の視覚的な表現はこのようになります。
lift関数のシリーズを使うと、コードがより読みやすくなります。
あらかじめ用意されたlift関数の1つを使うことで、<*>構文を避けられるからです。
まず、2引数関数を持ち上げる例を見てみましょう。
// テスト用の2引数関数を定義
let addPair x y = x + y
// 2引数関数を持ち上げる
let addPairOpt = Option.lift2 addPair
// 通常通り呼び出す
addPairOpt (Some 1) (Some 2)
// 結果 => Some 3
次に、3引数関数を持ち上げる例です。
// テスト用の3引数関数を定義
let addTriple x y z = x + y + z
// 3引数関数を持ち上げる
let addTripleOpt = Option.lift3 addTriple
// 通常通り呼び出す
addTripleOpt (Some 1) (Some 2) (Some 3)
// 結果 => Some 6
「lift2」を「結合器」として見る
applyには、関数適用とは別の見方があります。それは、高次の値を結合する「結合器」としての見方です。
たとえば、lift2を使う場合、最初のパラメータは組み合わせ方を指定します。
次の例では、同じ値を2つの異なる方法で組み合わています。最初は加算で、次は乗算です。
Option.lift2 (+) (Some 2) (Some 3) // Some 5
Option.lift2 (*) (Some 2) (Some 3) // Some 6
さらに一歩進んで、この最初の関数パラメータを取り除き、値を汎用的に組み合わせる方法はないでしょうか。
実はあります。タプルコンストラクタを使って値を組み合わせるのです。 こうすることで、値の使い方をまだ決めずに組み合わせられます。
図で表すとこんな感じです。
オプションとリスト用の実装例を見てみましょう。
// タプル作成関数を定義
let tuple x y = x,y
// タプルコンストラクタを組み込んだ
// オプション用の汎用結合器を作成
let combineOpt x y = Option.lift2 tuple x y
// タプルコンストラクタを組み込んだ
// リスト用の汎用結合器を作成
let combineList x y = List.lift2 tuple x y
これらの結合器を使うとどうなるか見てみましょう。
combineOpt (Some 1) (Some 2)
// 結果 => Some (1, 2)
combineList [1;2] [100;200]
// 結果 => [(1, 100); (1, 200); (2, 100); (2, 200)]
高次のタプルができたので、あとはmapを使って好きな方法でペアを処理できます。
値を足したいなら、map関数で+を使うだけです。
combineOpt (Some 2) (Some 3)
|> Option.map (fun (x,y) -> x + y)
// 結果 => Some 5
combineList [1;2] [100;200]
|> List.map (fun (x,y) -> x + y)
// 結果 => [101; 201; 102; 202]
値を掛けたいなら、map関数で*を使います。
combineOpt (Some 2) (Some 3)
|> Option.map (fun (x,y) -> x * y)
// 結果 => Some 6
combineList [1;2] [100;200]
|> List.map (fun (x,y) -> x * y)
// 結果 => [100; 200; 200; 400]
このように、様々な処理が可能です。実際の使用例では、もっと複雑な操作を行うでしょう。
lift2を使ってapplyを定義する
面白いことに、上記のlift2関数を使ってapplyを定義することもできます。
つまり、lift2関数を使ってapplyを定義できるのです。組み合わせ関数を単なる関数適用にするだけです。
Optionの場合、こんな感じになります。
module Option =
/// lift2をゼロから定義
let lift2 f xOpt yOpt =
match xOpt,yOpt with
| Some x,Some y -> Some (f x y)
| _ -> None
/// lift2を使ってapplyを定義
let apply fOpt xOpt =
lift2 (fun f x -> f x) fOpt xOpt
この別のアプローチは覚えておく価値があります。というのも、一部の型ではapplyよりもlift2を定義する方が簡単だからです。
欠けているデータや不正なデータの組み合わせ
注目すべき点として、これまで見てきたすべての結合器には共通点があります。高次の値のどれかが「欠けている」か「不正」な場合、全体の結果も不正になるのです。
たとえば、combineListでは、パラメータの1つが空リストの場合、結果も空リストになります。
combineOptでは、パラメータの1つがNoneの場合、結果もNoneになります。
combineOpt (Some 2) None
|> Option.map (fun (x,y) -> x + y)
// 結果 => None
combineList [1;2] []
|> List.map (fun (x,y) -> x * y)
// 結果 => 空リスト
欠けている値や不正な値を無視する別の種類の結合器を作ることも可能です。数値に「0」を足すのが無視されるのと同じような感じです。 詳しい情報は、「つらくないモノイド」に関する私の投稿をご覧ください。
片側結合器 <* と *>
場合によっては、2つの高次の値があり、どちらか一方の値を捨てたいことがあります。
リストの例を見てみましょう。
let ( <* ) x y =
List.lift2 (fun left right -> left) x y
let ( *> ) x y =
List.lift2 (fun left right -> right) x y
2要素のリストと3要素のリストを組み合わせると、期待通り6要素のリストができますが、内容は片側からだけ来ています。
[1;2] <* [3;4;5] // [1; 1; 1; 2; 2; 2]
[1;2] *> [3;4;5] // [3; 4; 5; 3; 4; 5]
これを機能として活用できます！ある値をN回繰り返すには、[1..n]と組み合わせるだけです。
let repeat n pattern =
[1..n] *> pattern
let replicate n x =
[1..n] *> [x]
repeat 3 ["a";"b"]
// ["a"; "b"; "a"; "b"; "a"; "b"]
replicate 5 "A"
// ["A"; "A"; "A"; "A"; "A"]
もちろん、これは値を複製する効率的な方法ではありません。
ただ、applyとreturnという2つの関数から始めて、かなり複雑な動作を構築できることを示しています。
では、より実用的な観点から、このような「データを捨てる」操作がなぜ役立つのでしょうか？多くの場合、値そのものは必要ないけれど、その効果は欲しい場合があります。
たとえば、パーサーでは次のようなコードをよく目にします。
let readQuotedString =
readQuoteChar *> readNonQuoteChars <* readQuoteChar
このスニペットで、readQuoteCharは「入力ストリームから引用符を見つけて読み取る」ことを意味し、
readNonQuoteCharsは「入力ストリームから引用符以外の文字列を読み取る」ことを意味します。
引用符で囲まれた文字列をパースする際、引用符を含む入力ストリームが確実に読み取られることを確認したいですが、 引用符自体には興味がなく、内部の内容だけが欲しいのです。
そのため、先頭の引用符を無視するために*>を使い、末尾の引用符を無視するために<*を使っています。
zip関数とZipList世界
一般的な名前 zip、zipWith、map2
一般的な演算子 <*>（ZipList世界の文脈で）
機能 指定された関数を使って2つのリスト（または他の列挙可能なもの）を組み合わせます
シグネチャ E<(a->b->c)> -> E<a> -> E<b> -> E<c>（Eはリストまたは他の列挙可能な型）、
またはタプルで組み合わせる版では E<a> -> E<b> -> E<a,b>
説明
一部のデータ型では、applyの有効な実装が複数存在する可能性があります。
たとえば、リストにはZipListや類似の名前でよく知られる、もう1つのapplyの実装があります。
この実装では、各リストの対応する要素が同時に処理され、次の要素に移るために両方のリストが一緒にシフトされます。
つまり、関数のリスト[f; g]を値のリスト[x; y]に適用すると、2要素のリスト[f x; g y]になります。
// 代替の「zip」実装
// [f;g] apply [x;y] は [f x; g y] になる
let rec zipList fList xList =
match fList,xList with
| [],_
| _,[] ->
// どちらかの側が空なら終了
[]
| (f::fTail),(x::xTail) ->
// 新しいhead + 新しいtail
(f x) :: (zipList fTail xTail)
// 型：('a -> 'b) -> 'a list -> 'b list
注意：この実装はデモンストレーション用です。末尾再帰ではないので、大きなリストには使用しないでください！
リストの長さが異なる場合の挙動は実装によって異なります。F#ライブラリ関数のList.map2やList.zipのように例外をスローするものもあれば、
上記の実装のように余分なデータを静かに無視するものもあります。
では、実際に使ってみましょう。
let add10 x = x + 10
let add20 x = x + 20
let add30 x = x + 30
let result =
let (<*>) = zipList
[add10; add20; add30] <*> [1; 2; 3]
// result => [11; 22; 33]
結果が[11; 22; 33]、つまり3要素だけになっていることに注目してください。標準のList.applyを使っていたら、9要素になっていたでしょう。
「zip」を「結合器」として解釈する
先ほどList.apply、より正確にはList.lift2を結合器として解釈できることを見ました。同様に、zipListも結合器として考えることができます。
let add x y = x + y
let resultAdd =
let (<*>) = zipList
[add;add] <*> [1;2] <*> [10;20]
// resultAdd = [11; 22]
// [ (add 1 10); (add 2 20) ]
最初のリストにadd関数を1つだけ入れることはできない点に注意してください。2番目と3番目のリストの各要素に対して1つのaddが必要になります！
このやり方は少し面倒かもしれません。そのため、よく使われるのがzipの「タプル化」バージョンです。このバージョンでは、結合関数を指定する必要がなく、代わりにタプルのリストが返されます。
このタプルのリストは、後からmapを使って処理できます。
これは、先ほど説明したcombine関数で用いたアプローチと同じですが、zipListに適用したものです。
ZipList世界
標準のリスト世界にはapplyとreturnがありますが、先ほど見た異なるバージョンのapplyを使うと、
ZipList世界と呼ばれる、リストの別バージョンの世界を作れます。
ZipList世界は標準のリスト世界とはかなり異なります。
ZipList世界のapply関数は先ほど説明したように実装されますが、より興味深いのはreturnの実装です。
ZipList世界のreturnは標準のリスト世界とはまったく異なり、
単一要素のリストではなく
無限に繰り返される値でなければなりません！
F#のような非遅延言語ではこれを直接実現できませんが、ListをSeq（別名IEnumerable）に置き換えれば、
次のように無限に繰り返される値を作成できます。
module ZipSeq =
// ZipSeq世界の"return"を定義
let retn x = Seq.initInfinite (fun _ -> x)
// ZipSeq世界の"apply"を定義
// （ここでは"lift2"、別名"map2"を使ってapplyを定義できます）
let apply fSeq xSeq =
Seq.map2 (fun f x -> f x) fSeq xSeq
// 型：('a -> 'b) seq -> 'a seq -> 'b seq
// 2つのシーケンスを組み合わせた新しいシーケンスを定義
let triangularNumbers =
let (<*>) = apply
let addAndDivideByTwo x y = (x + y) / 2
let numbers = Seq.initInfinite id
let squareNumbers = Seq.initInfinite (fun i -> i * i)
(retn addAndDivideByTwo) <*> numbers <*> squareNumbers
// 最初の10要素を評価し
// 結果を表示
triangularNumbers |> Seq.take 10 |> List.ofSeq |> printfn "%A"
// 結果 =>
// [0; 1; 3; 6; 10; 15; 21; 28; 36; 45]
この例は、高次の世界がデータ型（リスト型など）だけでなく、そのデータ型と共に働く関数で構成されることを示しています。 この特定のケースでは、「リスト世界」と「ZipList世界」は同じデータ型を共有していますが、かなり異なる環境を持っています。
どのような型がmapとapplyとreturnをサポートしているか？
ここまで、これらの便利な関数をすべて抽象的な方法で定義してきました。 では、これらの関数のすべて（および様々な法則）の実装を持つ実際の型を見つけるのは、どれほど簡単でしょうか？
答えは、とても簡単です！実際、ほとんどすべての型がこれらの関数のセットをサポートしています。むしろ、これらをサポートしていない有用な型を見つけるのが難しいほどです。
つまり、mapとapplyとreturnは、Option、List、Seq、Asyncなどの標準的な型で利用可能（または簡単に実装可能）であり、
さらに、あなたが自分で定義する可能性のある型でも同様にサポートできるということです。
まとめ
この投稿では、単純な「通常の」値を高次の世界に持ち上げるための3つのコア関数について説明しました。map、return、apply、
そしてliftNやzipのような派生関数です。
しかし実際には、事態はそれほど単純ではありません。世界をまたぐ関数を頻繁に扱う必要があるのです。 これらの関数の入力は通常の世界にありますが、出力は高次の世界にあります。
次の投稿では、これらの世界をまたぐ関数も高次の世界に持ち上げる方法を紹介します。