このシリーズの前回の投稿では、適切なモノイドだけを扱いました。

でも、扱いたいものがモノイドでない場合はどうすればいいでしょうか。 この投稿では、ほぼすべてのものをモノイドに変換するコツをお教えします。

その過程で、シングルトンよりもリストを好む、オプション型をできるだけ使うなど、重要でよく使われる関数型設計のイディオムをいくつか紹介します。

クロージャを得る

思い出してください。適切なモノイドには3つの条件が必要です。クロージャ、結合法則、単位元です。 各要件には課題があるので、順番に説明していきます。

まずはクロージャから始めましょう。

値を足し合わせたいけれど、結合した値の型が元の値の型と同じではない場合があります。 こんな場合、どう対処すればいいでしょうか。

一つの方法は、元の型から新しい型にマップすることです。前回の投稿で、CustomerとCustomerStatsの例でこのアプローチを使いました。 多くの場合、元の型の設計を変更する必要がないので、これが最も簡単なアプローチです。

一方で、mapを使いたくない場合もあります。最初からクロージャの要件を満たすように型を設計したい場合もあるでしょう。

いずれにせよ、新しい型を設計する場合でも、既存の型を再設計する場合でも、クロージャを得るには似たような技術を使えます。

クローズド型を組み合わせて新しい複合型を作る

数値型が加算や乗算などの基本的な数学演算でクローズドなのは明らかです。 文字列やリストなどの非数値型も、連結演算でクローズドなのを見てきました。

これを踏まえると、これらの型の組み合わせもクローズドになるのは明らかです。 コンポーネント型に適切な「加算」を行うように「加算」関数を定義するだけです。

例を見てみましょう。

type MyType = {count:int; items:int list}

let addMyType t1 t2 = 
    {count = t1.count + t2.count; 
     items = t1.items @ t2.items}

addMyType関数はintフィールドに整数加算を、listフィールドにリスト連結を使います。 結果として、MyTypeはaddMyType関数を使ってクローズドになります。実際、クローズドになるだけでなく、モノイドにもなります。これで完成です！

これは前回の投稿でCustomerStatsに用いたアプローチと同じです。

ここで最初のコツを紹介します。

• 設計のコツ：モノイド的な型を簡単に作るには、型の各フィールドもモノイドになるようにしましょう。

考えてみてください。この方法を使うとき、新しい複合型の「ゼロ」は何になりますか？

非数値型の扱い

上記のアプローチは複合型を作る際に有効です。でも、明らかな数値的等価物がない非数値型はどうすればいいでしょうか？

とてもシンプルな例を見てみましょう。次のように足し合わせたい文字がある場合を考えます。

'a' + 'b' -> what?

しかし、文字と文字を足しても別の文字にはなりません。強いて言えば、文字列になります。

'a' + 'b' -> "ab" // クロージャの失敗！

でも、これはクロージャの要件を満たさないので、とても役に立ちません。

この問題を解決する一つの方法は、文字を強制的に文字列にすることです。これは確かに機能します。

"a" + "b" -> "ab"

ただし、これは文字に特化した解決策です。他の型にも適用できる、より一般的な解決策はないでしょうか？

少し考えてみましょう。stringとcharの関係は何でしょうか。文字列は文字のリストまたは配列と考えることができます。

つまり、代わりに文字のリストを使うこともできます。

['a'] @ ['b'] -> ['a'; 'b'] // リスト万歳！

これもクロージャの要件を満たします。

さらに、これは実際にこの種の問題に対する一般的な解決策です。なぜなら、何でもリストに入れることができ、リスト（連結を伴う）は常にモノイドだからです。

ここで次のコツを紹介します。

• 設計のコツ：非数値型のクロージャを可能にするには、単一の項目をリストに置き換えましょう。

場合によっては、モノイドを設定するときにリストに変換し、終了時に別の型に変換する必要があるかもしれません。

たとえば、Charの場合、文字のリストですべての操作を行い、最後に文字列に変換するだけです。

では、「モノイド的な文字」モジュールを作ってみましょう。

module MonoidalChar =
    open System

    /// "モノイド的な文字"
    type MChar = MChar of Char list

    /// 文字を"モノイド的な文字"に変換する
    let toMChar ch = MChar [ch]

    /// 2つのモノイド的な文字を足す
    let addChar (MChar l1) (MChar l2) = 
        MChar (l1 @ l2)

    // 中置演算子版
    let (++) = addChar  

    /// 文字列に変換する
    let toString (MChar cs) = 
        new System.String(List.toArray cs)

MCharは単一の文字ではなく、文字のリストのラッパーになっています。

では、テストしてみましょう。

open MonoidalChar

// 2つの文字を足して文字列に変換する
let a = 'a' |> toMChar
let b = 'b' |> toMChar
let c = a ++ b
c |> toString |> printfn "a + b = %s"  
// 結果: "a + b = ab"

凝ってみたい場合は、map/reduceを使って文字のセットを処理することもできます。

[' '..'z']   // たくさんの文字を取得
|> List.filter System.Char.IsPunctuation
|> List.map toMChar
|> List.reduce addChar
|> toString
|> printfn "句読点は %s" 
// 結果: "句読点は !"#%&'()*,-./:;?@[\]_"

エラーのモノイド

MonoidalCharの例は些細なもので、他の方法でも実装できるかもしれません。しかし、一般的にこれは非常に便利な技術です。

たとえば、バリデーションを行うシンプルなモジュールを見てみましょう。SuccessとFailureの2つのオプションがあり、Failureの場合はエラー文字列も含まれます。

module Validation = 

    type ValidationResult = 
        | Success
        | Failure of string

    let validateBadWord badWord (name:string) =
        if name.Contains(badWord) then
            Failure ("文字列に悪い単語が含まれています: " + badWord)
        else 
            Success 

    let validateLength maxLength name =
        if String.length name > maxLength then
            Failure "文字列が長すぎます"
        else 
            Success

実際には、文字列に対して複数のバリデーションを行い、すべての結果を一度に返したいでしょう。何らかの方法で足し合わせたいのです。

これはモノイドを求めているのと同じです！2つの結果を対ごとに足せるなら、好きなだけ結果を足し合わせることができます！

そこで問題になるのが、2つのバリデーション結果をどう組み合わせるかです。

let result1 = Failure "文字列がnullまたは空です"
let result2 = Failure "文字列が長すぎます"

result1 + result2 = ????

単純なアプローチは文字列を連結することですが、フォーマット文字列やローカライゼーション用のリソースIDを使っている場合には機能しません。

いいえ、もっと良い方法は、Failureケースを単一の文字列ではなく文字列のリストを使うように変更することです。そうすれば、結果の組み合わせが簡単になります。

上記のコードをFailureケースがリストを使うように変更したものを見てみましょう。

module MonoidalValidation = 

    type ValidationResult = 
        | Success
        | Failure of string list

    // 単一の文字列をFailureケースに変換するヘルパー
    let fail str =
        Failure [str]

    let validateBadWord badWord (name:string) =
        if name.Contains(badWord) then
            fail ("文字列に悪い単語が含まれています: " + badWord)
        else 
            Success 

    let validateLength maxLength name =
        if String.length name > maxLength then
            fail "文字列が長すぎます"
        else 
            Success

個々のバリデーションが単一の文字列でfailを呼び出しているのがわかります。しかし、内部では文字列のリストとして保存され、後で連結できます。

これで、add関数を作成できます。

ロジックは次のようになります。

• 両方の結果がSuccessなら、組み合わせた結果もSuccessです。
• 一方の結果がFailureなら、組み合わせた結果はその失敗です。
• 両方の結果がFailureなら、組み合わせた結果は両方のエラーリストを連結したFailureです。

コードは次のようになります。

module MonoidalValidation = 

    // 上記と同じ

    /// 2つの結果を足す
    let add r1 r2 = 
        match r1,r2 with
        | Success,    Success -> Success 
        | Failure f1, Success -> Failure f1
        | Success,    Failure f2 -> Failure f2
        | Failure f1, Failure f2 -> Failure (f1 @ f2)

ロジックを確認するためのテストをいくつか見てみましょう。

open MonoidalValidation 

let test1 = 
    let result1 = Success
    let result2 = Success
    add result1 result2 
    |> printfn "結果は %A"
    // "結果は Success"

let test2 = 
    let result1 = Success
    let result2 = fail "文字列が長すぎます"
    add result1 result2 
    |> printfn "結果は %A"
    // "結果は Failure ["文字列が長すぎます"]"

let test3 = 
    let result1 = fail "文字列がnullまたは空です"
    let result2 = fail "文字列が長すぎます"
    add result1 result2 
    |> printfn "結果は %A"

    // 結果は Failure 
    //   [ "文字列がnullまたは空です"; 
    //     "文字列が長すぎます"]

そして、より現実的な例として、適用したいバリデーション関数のリストがある場合を見てみましょう。

let test4 = 
    let validationResults str = 
        [
        validateLength 10
        validateBadWord "monad"
        validateBadWord "cobol"
        ]
        |> List.map (fun validate -> validate str)

    "cobol has native support for monads"
    |> validationResults 
    |> List.reduce add
    |> printfn "結果は %A"

出力は3つのエラーメッセージを含むFailureです。

結果は Failure
  ["文字列が長すぎます"; "文字列に悪い単語が含まれています: monad";
   "文字列に悪い単語が含まれています: cobol"]

このモノイドを完成させるには、もう一つ必要なものがあります。「ゼロ」も必要です。何がゼロになるでしょうか？

定義上、他の結果と組み合わせたとき、その結果をそのまま残すものです。

この定義によれば、「ゼロ」は単にSuccessだとわかるはずです。

module MonoidalValidation = 

    // 上記と同じ

    // 単位元
    let zero = Success

ご存知の通り、reduceするリストが空の場合にzeroを使う必要があります。 そこで、バリデーション関数をまったく適用しない例を見てみましょう。これにより、空のValidationResultリストが得られます。

let test5 = 
    let validationResults str = 
        []
        |> List.map (fun validate -> validate str)

    "cobol has native support for monads"
    |> validationResults 
    |> List.fold add zero
    |> printfn "結果は %A"

    // 結果は Success

reduceをfoldに変更する必要もありました。そうしないと実行時エラーが発生します。

パフォーマンスのためのリスト

リストを使うメリットをもう一つ紹介しましょう。他の組み合わせ方法と比べて、リストの連結は計算量も消費メモリも比較的少なくて済みます。 これは、参照されているオブジェクトを変更したり再割り当てしたりする必要がないためです。

たとえば、前回の投稿では、文字列をラップしたTextブロックを定義し、その内容を連結するために文字列連結を使いました。

type Text = Text of string

let addText (Text s1) (Text s2) =
    Text (s1 + s2)

しかし、大きな文字列の場合、この連続的な連結は高コストになる可能性があります。

代わりに、Textブロックが文字列のリストを含むような実装を考えてみましょう。

type Text = Text of string list

let addText (Text s1) (Text s2) =
    Text (s1 @ s2)

実装はほとんど変わりませんが、パフォーマンスは大幅に向上する可能性があります。

文字列のリストで全ての操作を行い、処理の最後に通常の文字列に変換するだけで済みます。

リストのパフォーマンスでも不十分な場合は、ツリーやヒープなどの古典的なデータ構造や、ResizeArrayのような可変型を使用するように、このアプローチを簡単に拡張できます。 （パフォーマンスについての詳細は、この投稿の最後にある付録を参照してください）

専門用語注意

オブジェクトのリストをモノイドとして使用する概念は、数学では「自由モノイド」と呼ばれます。コンピュータサイエンスでは、 A*のような「クリーネスター」とも呼ばれます。空のリストを許可しない場合は、単位元がありません。この変種は「自由半群」またはA+のような「クリーネプラス」と呼ばれます。

この「スター」や「プラス」の表記は、正規表現を使ったことがある人なら見覚えがあるでしょう。*

_{* 正規表現とモノイドに関係があることに気づいていなかったかもしれません！さらに深い関係もあります。}

結合法則

クロージャを扱ったので、次は結合法則に取り組みましょう。

最初の投稿で、減算や除算など、結合法則を満たさない演算をいくつか見ました。

5 - (3 - 2)が(5 - 3) - 2と等しくないことから、減算が結合法則を満たさないことがわかります。 また、12 / (3 / 2)が(12 / 3) / 2と等しくないことから、除算も結合法則を満たさないことがわかります。

これらの場合、単一の正しい答えはありません。左から右に計算するか、右から左に計算するかによって、異なる答えが必要になる可能性があるからです。

実際、F#の標準ライブラリには、この好みに対応するためにfoldとreduceの2つのバージョンがあります。通常のfoldとreduceは左から右へ処理します。

//（12 - 3） - 2 と同じ
[12;3;2] |> List.reduce (-)  // => 7 

//（（12 - 3） - 2） - 1 と同じ
[12;3;2;1] |> List.reduce (-)  // => 6

一方、foldBackとreduceBackは右から左へ処理します。

//12 - （3 - 2）と同じ
[12;3;2] |> List.reduceBack (-) // => 11

//12 - （3 - （2 - 1））と同じ
[12;3;2;1] |> List.reduceBack (-) // => 10

ある意味、結合法則の要件は、foldを使ってもfoldBackを使っても同じ答えが得られるべきだと言っているのです。

演算を要素の中に移動する

しかし、一貫したモノイド的アプローチを望む場合、多くのケースでのコツは、演算を各要素のプロパティに移すことです。動詞としての演算ではなく、名詞としての演算にします。

たとえば、3 - 2は3 + (-2)と考えることができます。「減算」を動詞としてではなく、「マイナス2」を名詞として扱います。

この場合、上記の例は5 + (-3) + (-2)になります。 演算子として加算を使用しているので、結合法則が成り立ち、5 + (-3 + -2)は確かに(5 + -3) + -2と同じになります。

除算でも同様のアプローチが機能します。12 / 3 / 2は12 * (1/3) * (1/2)に変換でき、演算子は乗算になり、結合法則を満たします。

演算子をオブジェクトのプロパティに変換するこのアプローチは、うまく一般化できます。

ここで次のコツを紹介します。

• 設計のコツ：演算の結合法則を得るには、演算をオブジェクトの中に移すことを試みましょう。

これがどのように機能するかを理解するために、以前の例を再検討してみましょう。 最初の投稿で、文字列に対する結合法則を満たさない演算を考え出そうとして、subtractCharsに落ち着いたことを思い出してください。

subtractCharsの簡単な実装は次のとおりです。

let subtractChars (s1:string) (s2:string) = 
    let isIncluded (ch:char) = s2.IndexOf(ch) = -1
    let chars = s1.ToCharArray() |> Array.filter isIncluded
    System.String(chars)

// 中置演算子版        
let (--) = subtractChars

この実装で、いくつかの対話的なテストができます。

"abcdef" -- "abd"   //  "cef"
"abcdef" -- ""      //  "abcdef"

そして、結合法則の要件が満たされていないことを自分で確認できます。

("abc" -- "abc") -- "abc"  // ""
"abc" -- ("abc" -- "abc")  // "abc"

これをどうすれば結合法則を満たすようにできるでしょうか？

コツは、先ほどの数字の例と同様に、演算子から「引く」という性質をオブジェクトに移すことです。

つまり、プレーンな文字列を、「引く」または「削除する文字」というデータ構造に置き換えます。これは削除したいものを捕捉します。

let removalAction = (subtract "abd") // データ構造

そして、このデータ構造を文字列に「適用」します。

let removalAction = (subtract "abd") 
removalAction |> applyTo "abcdef"  // "結果は cef"

このアプローチを使えば、上記の結合法則を満たさない例を次のように書き直すことができます。

let removalAction = (subtract "abc") + (subtract "abc") + (subtract "abc")   
removalAction |> applyTo "abc"    // "結果は "

はい、元のコードと全く同じではありませんが、多くの状況でこの方が実際にはより適していると気づくかもしれません。

実装は以下の通りです。文字のセットを含むCharsToRemoveを定義し、他の関数の実装はそこから自然に導き出されます。

/// 削除する文字のリストを保存
type CharsToRemove = CharsToRemove of Set<char>

/// 新しいCharsToRemoveを構築
let subtract (s:string) = 
    s.ToCharArray() |> Set.ofArray |>  CharsToRemove 

/// CharsToRemoveを文字列に適用
let applyTo (s:string) (CharsToRemove chs) = 
    let isIncluded ch = Set.exists ((=) ch) chs |> not
    let chars = s.ToCharArray() |> Array.filter isIncluded
    System.String(chars)

// 2つのCharsToRemoveを組み合わせて新しいものを得る
let (++) (CharsToRemove c1) (CharsToRemove c2) = 
    CharsToRemove (Set.union c1 c2)

テストしてみましょう！

let test1 = 
    let removalAction = (subtract "abd") 
    removalAction |> applyTo "abcdef" |> printfn "結果は %s"
    // "結果は cef"

let test2 = 
    let removalAction = (subtract "abc") ++ (subtract "abc") ++ (subtract "abc")   
    removalAction |> applyTo "abcdef" |> printfn "結果は %s"
    // "結果は "

このアプローチの考え方は、ある意味で、データではなくアクションをモデル化していることです。CharsToRemoveアクションのリストがあり、 それらを単一の「大きな」CharsToRemoveアクションに組み合わせ、 中間的な操作が終わった後、最後にその単一のアクションを実行します。

すぐに別の例を見ますが、この時点で「これは関数に似ていますね？」と思うかもしれません。その通りです！

実際、このCharsToRemoveデータ構造を作る代わりに、元のsubtractChars関数を部分適用することもできました。以下のようになります。

（部分適用を容易にするためにパラメータの順序を逆にしていることに注意してください）

// 部分適用のために逆順に
let subtract str charsToSubtract = 
    subtractChars charsToSubtract str 

let removalAction = subtract "abd" 
"abcdef" |> removalAction |> printfn "結果は %s"
// "結果は cef"

これで特別なapplyTo関数さえ必要ありません。

しかし、このような減算関数が複数ある場合はどうすればいいでしょうか？ これらの部分適用された関数はそれぞれstring -> stringという型を持っているので、どのように「足し合わせる」ことができるでしょうか？

(subtract "abc") + (subtract "abc") + (subtract "abc")  = ?

答えは、もちろん関数合成です！

let removalAction2 = (subtract "abc") >> (subtract "abc") >> (subtract "abc") 
removalAction2 "abcdef" |> printfn "結果は %s"
// "結果は def"

これは、CharsToRemoveデータ構造を作成することの関数版です。

「データ構造としてのアクション」アプローチと関数アプローチは完全に同じではありません。CharsToRemoveアプローチはセットを使用し、最後にのみ文字列に適用されるため、より効率的かもしれません。しかし、両者とも同じ目標を達成します。 どちらが良いかは、取り組んでいる特定の問題に依存します。

次の投稿で、関数とモノイドについてさらに詳しく説明します。

単位元

最後にモノイドの要件である単位元について見ていきましょう。

これまで見てきたように、単位元は常に必要というわけではありませんが、空のリストを扱う可能性がある場合には便利です。

数値の場合、演算の単位元を見つけるのは一般的に簡単です。0（加算）、1（乗算）、Int32.MinValue（最大値）などです。

この考え方は、数値だけを含む構造にも適用できます。適切な値をすべて対応する単位元に設定するだけです。前回の投稿のCustomerStats型がその良い例です。

しかし、数値でないオブジェクトの場合はどうでしょうか？自然な候補がない場合、どのように「ゼロ」や単位元を作ればいいでしょうか？

答えは：適当に作ってしまうのです。

マジです！

前回の投稿で、OrderLine型にEmptyOrderケースを追加した例を見ました。

type OrderLine = 
    | Product of ProductLine
    | Total of TotalLine
    | EmptyOrder

これをもう少し詳しく見てみましょう。2つのステップを踏みました。

• まず、新しいケースを作成し、OrderLineの選択肢のリストに追加しました（上記のとおり）。
• 次に、addLine関数を調整して、それを考慮するようにしました（以下のとおり）。

let addLine orderLine1 orderLine2 =
    match orderLine1,orderLine2 with
    // どちらかがゼロ？その場合、もう一方を返す
    | EmptyOrder, _ -> orderLine2
    | _, EmptyOrder -> orderLine1
    // 他のケースのロジック...

これだけです。

新しく拡張された型は、古い注文行のケースに加えて、新しいEmptyOrderケースで構成されており、古いケースの振る舞いの多くを再利用できます。

特に、新しく拡張された型がすべてのモノイドの規則に従っていることがわかりますか？

• 新しい型の2つの値を足すと、新しい型の別の値が得られます（クロージャ）。
• 古い型で組み合わせの順序が問題なかった場合、新しい型でも順序は問題になりません（結合法則）。
• そして最後に... この追加のケースが新しい型の単位元を提供します。

PositiveNumberをモノイドに変える

これまで見てきた他の半群でも同じことができます。

たとえば、先ほど、正の数（加算の下で）には単位元がなく、半群にすぎないと述べました。 「追加のケースで拡張する」テクニック（単に0を使うのではなく！）を使って単位元を作りたい場合、 まず特別なZeroケース（整数ではない）を定義し、それを扱えるaddPositive関数を作成します。以下のようになります。

type PositiveNumberOrIdentity = 
    | Positive of int
    | Zero

let addPositive i1 i2 =
    match i1,i2 with
    | Zero, _ -> i2
    | _, Zero -> i1
    | Positive p1, Positive p2 -> Positive (p1 + p2)

確かに、PositiveNumberOrIdentityは人為的な例ですが、「通常の」値と特別な、別個のゼロ値がある状況で、このアプローチがどのように機能するかがわかります。

汎用的な解決策

これには2つの欠点があります。

• 通常のケースとゼロのケースの2つを扱う必要があります。
• カスタム型とカスタムの加算関数を作る必要があります。

残念ながら、最初の問題については何もできません。 自然なゼロがないシステムで人工的なゼロを作る場合、常に2つのケースを扱う必要があります。

しかし、2番目の問題については対処できます！新しいカスタム型を何度も作成する代わりに、 通常の値用と人工的なゼロ用の2つのケースを持つ汎用的な型を作成できないでしょうか？以下のようになります。

type NormalOrIdentity<'T> = 
    | Normal of 'T
    | Zero

この型は見覚えがありませんか？これは単にオプション型の変装です！

言い換えれば、通常の値の集合の外にある単位元が必要な場合はいつでも、Option.Noneを使ってそれを表現できます。そして、他のすべての「通常の」値にはOption.Someを使います。

Optionを使うもう一つの利点は、完全に汎用的な「加算」関数も書けることです。最初の試みは以下のようになります。

let optionAdd o1 o2 =
    match o1, o2 with
    | None, _ -> o2
    | _, None -> o1
    | Some s1, Some s2 -> Some (s1 + s2)

ロジックは簡単です。どちらかのオプションがNoneなら、もう一方のオプションを返します。両方がSomeなら、中身を取り出して足し、再びSomeでラップします。

しかし、最後の行の+は足し合わせる型について仮定をしています。加算関数を明示的に渡す方が良いでしょう。以下のようになります。

let optionAdd f o1 o2 =
    match o1, o2 with
    | None, _ -> o2
    | _, None -> o1
    | Some s1, Some s2 -> Some (f s1 s2)

実際には、部分適用を使って加算関数を組み込むことになります。

ここで、もう一つ重要なコツを紹介します。

• 設計のコツ：演算の単位元を得るには、判別共用体に特別なケースを作るか、もっと簡単に、オプションを使いましょう。

PositiveNumberの再検討

では、PositiveNumber の例を、今度はOption型を使って再度見てみましょう。

type PositiveNumberOrIdentity = int option
let addPositive = optionAdd (+)

とてもシンプルになりました！

optionAddに「実際の」加算関数をパラメータとして渡し、組み込んでいることに注目してください。 他の状況でも、半群に関連する適切な集約関数を同じように渡します。

この部分適用の結果、addPositiveの型シグネチャはint option -> int option -> int optionとなり、これはまさにモノイドの加算関数に期待されるものです。

言い換えれば、optionAddは任意の関数'a -> 'a -> 'aを、同じ関数ですがオプション型に「持ち上げられた」、つまり'a option -> 'a option -> 'a optionという型シグネチャを持つ関数に変換します。

では、テストしてみましょう！テストコードは以下のようになります。

// 値を作成
let p1 = Some 1
let p2 = Some 2
let zero = None

// 加算をテスト
addPositive p1 p2
addPositive p1 zero
addPositive zero p2
addPositive zero zero

残念ながら、Noneを単位元として得るために、通常の値をSomeでラップする必要があることがわかります。

これは面倒に聞こえるかもしれませんが、実際にはそれほど大変ではありません。 以下のコードは、リストの総和を求める際の2つの異なるケース、つまり空でないリストと空のリストの扱い方を示しています。

[1..10]
|> List.map Some
|> List.fold addPositive zero 

[]
|> List.map Some
|> List.fold addPositive zero

ValidationResultの再検討

ついでに、クロージャを得るためにリストを使う方法を説明したときに紹介したValidationResult型も再検討してみましょう。以下が再掲です。

type ValidationResult = 
    | Success
    | Failure of string list

正の整数の例から得た洞察を活かして、この型を別の角度から見てみましょう。

この型には2つのケースがあります。1つのケースはデータを保持し、もう1つのケースはデータを保持しません。しかし、本当に気にかけるべきデータはエラーメッセージであり、成功ではありません。 レフ・トルストイがほぼ言ったように、「すべての検証の成功は似ているが、各検証の失敗はそれぞれ独自の方法で失敗する」のです。

そこで、「結果」として考えるのではなく、この型を失敗を格納するものとして考え、次のように書き直してみましょう。失敗のケースを最初に置きます。

type ValidationFailure = 
    | Failure of string list
    | Success

この型が見覚えがありますか？

そうです！またもやオプション型です！この厄介なものから逃れられないのでしょうか？

オプション型を使えば、ValidationFailure型の設計を次のように簡略化できます。

type ValidationFailure = string list option

文字列を失敗のケースに変換するヘルパーは、リストを含むSomeになります。

let fail str =
    Some [str]

そして、「加算」関数はoptionAddを再利用できますが、今回は基本の演算としてリストの連結を使います。

let addFailure f1 f2 = optionAdd (@) f1 f2

最後に、元の設計でSuccessケースだった「ゼロ」は、新しい設計では単にNoneになります。

以下は全コードとテストです。

module MonoidalValidationOption = 

    type ValidationFailure = string list option

    // 文字列を失敗のケースに変換するヘルパー
    let fail str =
        Some [str]

    let validateBadWord badWord (name:string) =
        if name.Contains(badWord) then
            fail ("文字列に悪い単語が含まれています: " + badWord)
        else 
            None

    let validateLength maxLength name =
        if String.length name > maxLength then
            fail "文字列が長すぎます"
        else 
            None

    let optionAdd f o1 o2 =
        match o1, o2 with
        | None, _ -> o2
        | _, None -> o1
        | Some s1, Some s2 -> Some (f s1 s2)

    /// optionAddを使って2つの結果を足す
    let addFailure f1 f2 = optionAdd (@) f1 f2

    // ゼロを定義
    let Success = None

module MonoidalValidationOptionTest =
    open MonoidalValidationOption 

    let test1 = 
        let result1 = Success
        let result2 = Success
        addFailure result1 result2 
        |> printfn "結果は %A"

        // 結果は <null>

    let test2 = 
        let result1 = Success
        let result2 = fail "文字列が長すぎます"
        addFailure result1 result2 
        |> printfn "結果は %A"
        // 結果は Some ["文字列が長すぎます"]

    let test3 = 
        let result1 = fail "文字列がnullまたは空です"
        let result2 = fail "文字列が長すぎます"
        addFailure result1 result2 
        |> printfn "結果は %A"
        // 結果は Some ["文字列がnullまたは空です"; "文字列が長すぎます"]

    let test4 = 
        let validationResults str = 
            [
            validateLength 10
            validateBadWord "monad"
            validateBadWord "cobol"
            ]
            |> List.map (fun validate -> validate str)

        "cobol has native support for monads"
        |> validationResults 
        |> List.reduce addFailure
        |> printfn "結果は %A"
        // 結果は Some
        //   ["文字列が長すぎます"; "文字列に悪い単語が含まれています: monad";
        //    "文字列に悪い単語が含まれています: cobol"]

    let test5 = 
        let validationResults str = 
            []
            |> List.map (fun validate -> validate str)

        "cobol has native support for monads"
        |> validationResults 
        |> List.fold addFailure Success
        |> printfn "結果は %A"
        // 結果は <null>

設計のコツのまとめ

ここで一旦立ち止まって、これまでに扱ったことを振り返ってみましょう。

以下が全ての設計のコツをまとめたものです。

• モノイド的な型を簡単に作るには、型の各フィールドもモノイドになるようにしましょう。
• 非数値型のクロージャを可能にするには、単一の項目をリスト（または類似のデータ構造）に置き換えましょう。
• 演算の結合法則を得るには、演算をオブジェクトの中に移すことを試みましょう。
• 演算の単位元を得るには、判別共用体に特別なケースを作るか、もっと簡単に、オプションを使いましょう。

次の2つのセクションでは、これらのコツを前回の投稿で見た2つの非モノイド、「平均」と「最頻出単語」に適用してみましょう。

ケーススタディ：平均

さて、厄介な平均のケースを扱うためのツールキットができました。

以下は、ペアワイズ平均関数の簡単な実装です。

let avg i1 i2 = 
    float (i1 + i2) / 2.0

// テスト
avg 4 5 |> printfn "平均は %g"
// 平均は 4.5

最初の投稿で少し触れたように、avgはモノイドの3つの要件すべてを満たしていません！

まず、クローズドではありません。avgを使って組み合わせた2つのintは、別のintにはなりません。

次に、クローズドだったとしても、avgは結合法則を満たしません。以下のように類似のfloat関数avgfを定義すると、それがわかります。

let avgf i1 i2 = 
    (i1 + i2) / 2.0

// テスト
avgf (avgf 1.0 3.0) 5.0  |> printfn "左からの平均は %g"
avgf 1.0 (avgf 3.0 5.0)  |> printfn "右からの平均は %g"

// 左からの平均は 3.5
// 右からの平均は 2.5

最後に、単位元がありません。

どの数と平均を取っても元の値を返す数は何でしょうか？答え：ありません！

設計のコツを適用する

では、設計のコツを適用して、解決策を見つけられるか試してみましょう。

• モノイド的な型を簡単に作るには、型の各フィールドもモノイドになるようにしましょう。

「平均」は数学的な演算なので、モノイド的な等価物も数字に基づいていると予想できます。

• 非数値型のクロージャを可能にするには、単一の項目をリストに置き換えましょう。

一見したところ、これは関係なさそうなので、今のところスキップします。

• 演算の結合法則を得るには、演算をオブジェクトの中に移すことを試みましょう。

ここが肝心です！「平均」を動詞（演算）から名詞（データ構造）にどのように変換すればいいでしょうか？

答えは、実際の平均ではなく、「遅延平均」- 必要に応じて平均を計算するために必要なすべてのもの - を表すような構造を作ることです。

つまり、2つの要素を持つデータ構造が必要です：合計と数。この2つの数字があれば、必要に応じて平均を計算できます。

// 平均に必要なすべての情報を保存
type Avg = {total:int; count:int}

// 2つのAvgを足す
let addAvg avg1 avg2 = 
    {total = avg1.total + avg2.total; 
     count = avg1.count + avg2.count}

この構造の良いところは、floatではなくintを保存しているので、精度の損失やfloatの結合法則について心配する必要がないことです。

最後のコツは：

• 演算の単位元を得るには、判別共用体に特別なケースを作るか、もっと簡単に、オプションを使いましょう。

この場合、コツは必要ありません。2つの要素をゼロに設定することで簡単に単位元を作れるからです。

let zero = {total=0; count=0}

Noneを単位元として使うこともできましたが、この場合は過剰のように思えます。リストが空の場合でも、除算はできなくてもAvgの結果は有効です。

このデータ構造についての洞察を得たら、残りの実装は簡単に導き出せます。以下は全コードとテストです。

module Average = 

    // 平均に必要なすべての情報を保存
    type Avg = {total:int; count:int}

    // 2つのAvgを足す
    let addAvg avg1 avg2 = 
        {total = avg1.total + avg2.total; 
         count = avg1.count + avg2.count}

    // 加算のインライン版
    let (++) = addAvg

    // 単一の数字から平均を構築
    let avg n = {total=n; count=1}

    // データから平均を計算
    // 空のリストの場合は0を返す
    let calcAvg avg = 
        if avg.count = 0 
        then 0.0  
        else float avg.total / float avg.count

    // 代替案 - 空のリストの場合はNoneを返す
    let calcAvg2 avg = 
        if avg.count = 0 
        then None
        else Some (float avg.total / float avg.count)

    // 単位元
    let zero = {total=0; count=0}

    // テスト
    addAvg (avg 4) (avg 5) 
    |> calcAvg 
    |> printfn "平均は %g"
    // 平均は 4.5

    (avg 4) ++ (avg 5) ++ (avg 6) 
    |> calcAvg 
    |> printfn "平均は %g"
    // 平均は 5

    // テスト
    [1..10]
    |> List.map avg
    |> List.reduce addAvg
    |> calcAvg
    |> printfn "平均は %g"
    // 平均は 5.5

上記のコードでは、Avg構造を使って（浮動小数点の）平均を計算するcalcAvg関数を作成しました。このアプローチの良い点は、 ゼロ除算をどう扱うかの決定を遅らせられることです。単に0を返すこともできますし、あるいはNoneを返すこともできます。 または計算を無期限に延期し、必要になった時点で、オンデマンドで平均を生成することもできます！

そしてもちろん、この「平均」の実装には増分平均を行う能力があります。これはモノイドだからこそ無料で得られる機能です。

つまり、すでに100万個の数の平均を計算していて、もう1つ追加したい場合、すべてを再計算する必要はありません。 新しい数字をこれまでの合計に追加するだけでいいのです。

メトリクスに関する小さな余談

サーバーやサービスの管理を担当したことがある人なら、 CPU、I/Oなどのメトリクスのロギングとモニタリングの重要性を知っているでしょう。

そこでよく直面する質問の1つは、メトリクスをどのように設計するかということです。 1秒あたりのキロバイト数が欲しいのか、それともサーバー起動からの合計キロバイト数が欲しいのか。1時間あたりの訪問者数か、それとも合計訪問者数か。

メトリクス作成時のガイドラインを見ると、レートではなくカウンターのみを追跡するようにという頻繁な推奨事項があります。

カウンターの利点は、（a）データの欠損が全体像に影響を与えないこと、（b）後から様々な方法で集計できること - 分単位、時間単位、他のものとの比率など - です。

このシリーズを通じて学んできたことから、この推奨事項を本当はメトリクスはモノイドであるべきと言い換えられることがわかります。

上記のコードで「平均」を2つの要素、「合計」と「数」に変換する作業は、まさに良いメトリクスを作るために行うべきことです。

平均や他のレートはモノイドではありませんが、「合計」と「数」はモノイドであり、そこから好きな時に「平均」を計算できます。

ケーススタディ：「最頻出単語」をモノイドの準同型に変える

前回の投稿で、「最頻出単語」関数を実装しましたが、それがモノイドの準同型ではないことがわかりました。つまり、

mostFrequentWord(text1) + mostFrequentWord(text2)

は以下と同じ結果にはなりませんでした。

mostFrequentWord( text1 + text2 )

ここでも、設計のコツを使ってこれを修正し、うまく機能するようにできます。

ここでの洞察は、「平均」の例と同様に、計算を最後の瞬間まで遅らせることです。

そこで、最頻出単語を前もって計算するのではなく、後で最頻出単語を計算するために必要なすべての情報を保存するデータ構造を作ります。

module FrequentWordMonoid = 

    open System 
    open System.Text.RegularExpressions

    type Text = Text of string

    let addText (Text s1) (Text s2) =
        Text (s1 + s2)

    // 単語頻度マップを返す
    let wordFreq (Text s) =
        Regex.Matches(s,@"\S+")
        |> Seq.cast<Match>
        |> Seq.map (fun m -> m.ToString())
        |> Seq.groupBy id
        |> Seq.map (fun (k,v) -> k,Seq.length v)
        |> Map.ofSeq

上記のコードでは、単一の単語ではなくMap<string,int>を返す新しい関数wordFreqがあります。 つまり、各スロットに単語とそれに関連する頻度を持つ辞書を扱っています。

これがどのように機能するかのデモを見てみましょう。

module FrequentWordMonoid = 

    // 上記のコード

    let page1() = 
        List.replicate 1000 "hello world "
        |> List.reduce (+)
        |> Text

    let page2() = 
        List.replicate 1000 "goodbye world "
        |> List.reduce (+)
        |> Text

    let page3() = 
        List.replicate 1000 "foobar "
        |> List.reduce (+)
        |> Text

    let document() = 
        [page1(); page2(); page3()]

    // いくつかの単語頻度マップを表示
    page1() |> wordFreq |> printfn "page1の頻度マップは %A"
    page2() |> wordFreq |> printfn "page2の頻度マップは %A"

    //page1の頻度マップは map [("hello", 1000); ("world", 1000)]
    //page2の頻度マップは map [("goodbye", 1000); ("world", 1000)]

    document() 
    |> List.reduce addText
    |> wordFreq 
    |> printfn "文書全体の頻度マップは %A"

    //文書全体の頻度マップは map [
    //      ("foobar", 1000); ("goodbye", 1000); 
    //      ("hello", 1000); ("world", 2000)]

このマップ構造ができたので、2つのマップを足すaddMap関数を作れます。これは単に両方のマップから単語の頻度カウントをマージします。

module FrequentWordMonoid = 

    // 上記のコード

    // マップの加算を定義
    let addMap map1 map2 =
        let increment mapSoFar word count = 
            match mapSoFar |> Map.tryFind word with
            | Some count' -> mapSoFar |> Map.add word (count + count') 
            | None -> mapSoFar |> Map.add word count 

        map2 |> Map.fold increment map1

そして、すべてのマップを組み合わせた後、マップをループして最大の頻度を持つ単語を見つけることで、最頻出単語を計算できます。

module FrequentWordMonoid = 

    // 上記のコード

    // 最後のステップとして、
    // マップ内の最頻出単語を取得
    let mostFrequentWord map = 
        let max (candidateWord,maxCountSoFar) word count =
            if count > maxCountSoFar
            then (word,count)
            else (candidateWord,maxCountSoFar) 

        map |> Map.fold max ("None",0)

では、新しいアプローチを使って2つのシナリオを再検討してみましょう。

最初のシナリオは、すべてのページを単一のテキストに組み合わせ、wordFreqを適用して頻度マップを取得し、mostFrequentWordを適用して最頻出単語を取得します。

2番目のシナリオは、各ページに個別にwordFreqを適用して、各ページのマップを取得します。 これらのマップはaddMapで組み合わされて単一のグローバルマップになります。そして、前と同様に最後のステップとしてmostFrequentWordが適用されます。

module FrequentWordMonoid = 

    // 上記のコード

    document() 
    |> List.reduce addText
    |> wordFreq
    // 大きなマップから最頻出単語を取得
    |> mostFrequentWord
    |> printfn "先に加算を行うと、最頻出単語とその出現回数は %A"

    //先に加算を行うと、最頻出単語とその出現回数は ("world", 2000)

    document() 
    |> List.map wordFreq
    |> List.reduce addMap
    // より小さなマップをマージしてから最頻出単語を取得
    |> mostFrequentWord
    |> printfn "マップリデュースを使うと、最頻出単語とその出現回数は %A"

    //マップリデュースを使うと、最頻出単語とその出現回数は ("world", 2000)

このコードを実行すると、今度は同じ答えが得られることがわかります。

これは、wordFreqが実際にモノイドの準同型であり、並列実行や増分的な実行に適していることを意味します。

次回予告

この投稿では多くのコードを見てきましたが、すべてデータ構造に焦点を当てたものでした。

しかし、モノイドの定義には、組み合わせるものがデータ構造でなければならないという制約はありません - 何でも構いません。

次回の投稿では、型、関数、その他のオブジェクトに適用されるモノイドについて見ていきます。

付録：パフォーマンスについて

上記の例では、+が2つの数字を足すのと同じように、@を使って2つのリストを「足す」ことをよく行いました。 これは、数値の加算や文字列の連結など、他のモノイド的な演算との類似性を強調するためでした。

上記のコードサンプルが教育目的のものであり、必ずしも実際の本番環境で必要な、実戦で鍛えられた、往々にして美しくないコードのモデルとしては適していないことは明らかだと思います。

リストの連結（@）の使用は一般的に避けるべきだと指摘する人もいるでしょう。これは、最初のリスト全体をコピーする必要があり、あまり効率的ではないためです。

リストに何かを追加する最も良い方法は、いわゆる「cons」メカニズムを使って先頭に追加することです。F#では単に::を使います。F#のリストは連結リストとして実装されているので、 先頭への追加は非常に安価です。

このアプローチを使う問題は、対称的でないことです - 2つのリストを足すのではなく、リストと要素を足すだけです。これはモノイドの「加算」演算として使用できません。

分割統治のようなモノイドの利点が必要ない場合は、これは完全に有効な設計決定です。利益を得られないパターンのためにパフォーマンスを犠牲にする必要はありません。

@を使用する他の代替案は、そもそもリストを使わないことです！

リストの代替案

ValidationResultの設計では、結果の簡単な蓄積を得るために、エラー結果を保持するリストを使用しました。 しかし、list型を選んだのは、それがF#のデフォルトのコレクション型だからに過ぎません。 シーケンス、配列、セットなど、他のほとんどどのコレクション型を選んでも同じように機能したでしょう。

しかし、すべての型が同じパフォーマンスを持つわけではありません。たとえば、2つのシーケンスの組み合わせは遅延操作です。すべてのデータをコピーする必要はなく、一方のシーケンスを列挙し、次に他方を列挙するだけです。 そのため、おそらくより高速かもしれません。

推測するよりも、様々なリストサイズで、様々なコレクション型のパフォーマンスを測定する小さなテストスクリプトを書きました。

非常にシンプルなモデルを選びました：各オブジェクトが1つの項目を含むコレクションである、オブジェクトのリストがあります。 次に、適切なモノイド演算を使って、このコレクションのリストを単一の巨大なコレクションに縮約します。最後に、巨大なコレクションを一度反復処理します。

これはValidationResultの設計と非常によく似ています。そこでは、すべての結果を単一の結果リストに組み合わせ、そして（おそらく）エラーを表示するためにそれらを反復処理します。

これは「最頻出単語」の設計とも似ています。そこでは、個々の頻度マップをすべて単一の頻度マップに組み合わせ、最頻出単語を見つけるためにそれを反復処理します。 もちろん、その場合はmapを使用していましたが、ステップのセットは同じです。

パフォーマンス実験

では、コードを見てみましょう：

module Performance =

    let printHeader() =
        printfn "ラベル,リストサイズ,縮約と反復にかかったミリ秒" 

    // 与えられたリストサイズに対して縮約と反復のステップの時間を計測し、結果を出力
    let time label reduce iter listSize = 
        System.GC.Collect() //開始前にクリーンアップ
        let stopwatch = System.Diagnostics.Stopwatch()
        stopwatch.Start()
        reduce() |> iter
        stopwatch.Stop()
        printfn "%s,%iK,%i" label (listSize/1000) stopwatch.ElapsedMilliseconds 

    let testListPerformance listSize = 
        let lists = List.init listSize (fun i -> [i.ToString()])
        let reduce() = lists |> List.reduce (@) 
        let iter = List.iter ignore
        time "List.@" reduce iter listSize 

    let testSeqPerformance_Append listSize = 
        let seqs = List.init listSize (fun i -> seq {yield i.ToString()})
        let reduce() = seqs |> List.reduce Seq.append 
        let iter = Seq.iter ignore
        time "Seq.append" reduce iter listSize 

    let testSeqPerformance_Yield listSize = 
        let seqs = List.init listSize (fun i -> seq {yield i.ToString()})
        let reduce() = seqs |> List.reduce (fun x y -> seq {yield! x; yield! y})
        let iter = Seq.iter ignore
        time "seq(yield!)" reduce iter listSize 

    let testArrayPerformance listSize = 
        let arrays = List.init listSize (fun i -> [| i.ToString() |])
        let reduce() = arrays |> List.reduce Array.append 
        let iter = Array.iter ignore
        time "Array.append" reduce iter listSize 

    let testResizeArrayPerformance listSize  = 
        let resizeArrays = List.init listSize (fun i -> new ResizeArray<string>( [i.ToString()] ) ) 
        let append (x:ResizeArray<_>) y = x.AddRange(y); x
        let reduce() = resizeArrays |> List.reduce append 
        let iter = Seq.iter ignore
        time "ResizeArray.append" reduce iter listSize

コードを簡単に説明しましょう：

• time関数は縮約と反復のステップの時間を計測します。意図的にコレクションの作成にかかる時間は測定しません。 開始前にGCを実行していますが、実際には特定の型やアルゴリズムが引き起こすメモリ圧力は、それを使用する（または使用しない）決定の重要な部分です。 GCの仕組みを理解することは、パフォーマンスの高いコードを得るための重要な部分です。
• testListPerformance関数はコレクションのリスト（この場合はリスト）を設定し、reduceとiter関数も設定します。その後、reduceとiterに対してタイマーを実行します。
• 他の関数も同じことを行いますが、シーケンス、配列、ResizeArray（標準の.NETリスト）を使用します。 興味深いことに、シーケンスをマージする2つの方法をテストしてみました。 1つは標準ライブラリの関数Seq.appendを使用し、もう1つは2つのyield!を連続して使用します。
• testResizeArrayPerformanceはResizeArrayを使用し、右のリストを左のリストに追加します。 左のリストは変更され、必要に応じて大きくなり、成長戦略を使用して挿入を効率的に保ちます。

では、様々なサイズのリストでパフォーマンスをチェックするコードを書いてみましょう。2000から始めて、4000ずつ増やして50000まで行くことにしました。

open Performance

printHeader() 

[2000..4000..50000]
|> List.iter testArrayPerformance 

[2000..4000..50000]
|> List.iter testResizeArrayPerformance 

[2000..4000..50000]
|> List.iter testListPerformance

[2000..4000..50000]
|> List.iter testSeqPerformance_Append 

[2000..4000..50000]
|> List.iter testSeqPerformance_Yield

詳細な出力はすべて列挙しません - 自分でコードを実行できますが - 結果のグラフを以下に示します。

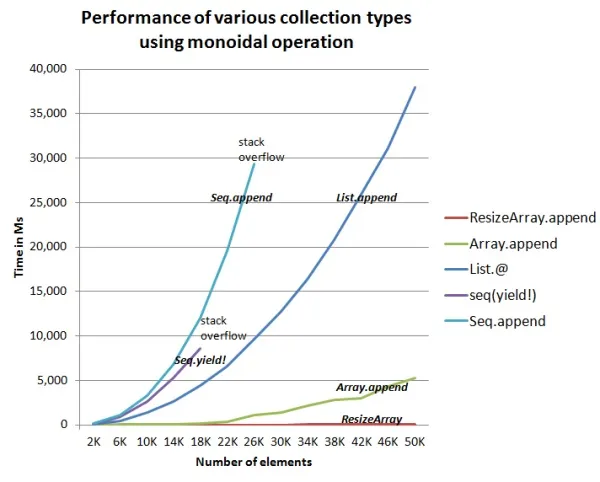
いくつか注目すべき点があります：

• 2つのシーケースベースの例はスタックオーバーフローでクラッシュしました。yield!はSeq.appendより約30%高速でしたが、より早くスタックを使い果たしました。
• List.appendはスタックオーバーフローしませんでしたが、リストが大きくなるにつれてかなり遅くなりました。
• Array.appendは高速で、リストのサイズが大きくなるにつれてより緩やかに増加しました。
• ResizeArrayが最も高速で、大きなリストでも問題ありませんでした。

クラッシュしなかった3つのコレクション型については、100Kアイテムのリストでも時間を計測しました。結果は以下の通りです：

• リスト = 150,730 ms
• 配列 = 26,062 ms
• ResizeArray = 33 ms

明らかな勝者がいますね。

結果の分析

この小さな実験からどのような結論を導き出せるでしょうか？

まず、こんな疑問が浮かぶかもしれません。デバッグモードでテストしたの？リリースモードでテストしたの？最適化はオンにしていたの？並列処理を使ってパフォーマンスを向上させることはできないの？ そして間違いなく、「なぜテクニックXを使ったの？テクニックYの方がずっと良いのに」というコメントがあるでしょう。

でも、ここで私が導き出したい結論はこうです：

• これらの結果から結論を導き出すことはできません！

状況によって異なるアプローチが必要です：

• 小さなデータセットを扱っている場合は、そもそもパフォーマンスを気にする必要がないかもしれません。この場合、リストを使い続けるでしょう - 必要がない限り、パターンマッチングや不変性を犠牲にしたくありません。
• パフォーマンスのボトルネックはリストの加算コードにはないかもしれません。実際にディスクI/Oやネットワーク遅延に時間を費やしているなら、リストの加算の最適化に取り組んでも意味がありません。 単語頻度の例の実世界版では、実際にはリストの加算よりも、ディスクからの読み取りや解析に多くの時間を費やす可能性があります。
• Google、Twitter、Facebookのような規模で作業している場合は、本当にアルゴリズムの専門家を雇う必要があります。

最適化とパフォーマンスに関する議論から導き出せる唯一の原則は以下の通りです：

• 問題は独自の文脈で扱わなければなりません。 処理されるデータのサイズ、ハードウェアの種類、メモリ量など、すべてがパフォーマンスに影響を与えます。 私にとって有効なことがあなたには有効でない可能性があります。だからこそ...
• 常に推測ではなく、測定しましょう。 コードがどこで時間を費やしているかについて仮定を立てないでください - プロファイラの使い方を学びましょう！ プロファイラの使用例はこことここにあります。
• マイクロ最適化に注意しましょう。プロファイラが、ソートルーチンが文字列の比較にすべての時間を費やしていることを示したとしても、必ずしも文字列比較関数を改善する必要があるとは限りません。 そもそも比較回数を減らすようにアルゴリズムを改善する方が良いかもしれません。早すぎる最適化などがそれに当たります。