実践におけるモノイド

前回の投稿では、モノイドの定義について見てきました。今回は、モノイドの実装方法を見ていきます。

まず、定義を振り返ってみましょう。

モノイドは、いくつかのものと、それらを2つずつ組み合わせる方法から始まります。
規則1（閉性）：2つのものを組み合わせた結果は、必ず元のもののうちの1つになります。
規則2（結合性）：3つ以上のものを組み合わせる場合、どの順序で2つずつ組み合わせても結果は同じになります。
規則3（単位元）：「ゼロ」と呼ばれる特別なものがあり、任意のものと「ゼロ」を組み合わせると、元のものが得られます。

たとえば、文字列をものとし、文字列の連結を操作とすると、モノイドになります。以下のコードでこれを示します。

let s1 = "hello"
let s2 = " world!"

// 閉性
let sum = s1 + s2  // sumは文字列

// 結合性
let s3 = "x"
let s4a = (s1+s2) + s3
let s4b = s1 + (s2+s3)
assert (s4a = s4b)

// 空文字列が単位元
assert (s1 + "" = s1)
assert ("" + s1 = s1)

では、これをより複雑なオブジェクトに適用してみましょう。

たとえば、OrderLineという構造体があるとします。これは販売注文の1行を表すものです。

type OrderLine = {
    ProductCode: string
    Qty: int
    Total: float
    }

そして、注文の合計を求めたいとします。つまり、複数の行のTotalフィールドを合計したいのです。

標準的な命令型アプローチでは、ローカルのtotal変数を作成し、行をループしながら合計していきます。以下のようになります。

let calculateOrderTotal lines =
    let mutable total = 0.0
    for line in lines do
        total <- total + line.Total
    total

試してみましょう。

module OrdersUsingImperativeLoop =

    type OrderLine = {
        ProductCode: string
        Qty: int
        Total: float
        }

    let calculateOrderTotal lines =
        let mutable total = 0.0
        for line in lines do
            total <- total + line.Total
        total

    let orderLines = [
        {ProductCode="AAA"; Qty=2; Total=19.98}
        {ProductCode="BBB"; Qty=1; Total=1.99}
        {ProductCode="CCC"; Qty=3; Total=3.99}
        ]

    orderLines
    |> calculateOrderTotal
    |> printfn "Total is %g"

しかし、経験豊富な関数型プログラマーなら、calculateOrderTotalでfoldを使うでしょう。以下のようになります。

module OrdersUsingFold =

    type OrderLine = {
        ProductCode: string
        Qty: int
        Total: float
        }

    let calculateOrderTotal lines =
        let accumulateTotal total line =
            total + line.Total
        lines
        |> List.fold accumulateTotal 0.0

    let orderLines = [
        {ProductCode="AAA"; Qty=2; Total=19.98}
        {ProductCode="BBB"; Qty=1; Total=1.99}
        {ProductCode="CCC"; Qty=3; Total=3.99}
        ]

    orderLines
    |> calculateOrderTotal
    |> printfn "Total is %g"

ここまでは順調です。では、モノイドアプローチを使った解決策を見てみましょう。

モノイドでは、何らかの加算や結合操作を定義する必要があります。以下のようなものはどうでしょうか？

let addLine orderLine1 orderLine2 =
    orderLine1.Total + orderLine2.Total

しかし、これではダメです。モノイドの重要な側面を忘れています。加算は同じ型の値を返す必要があります！

addLine関数のシグネチャを見てみると…

addLine : OrderLine -> OrderLine -> float

…戻り値の型がfloatで、OrderLineではありません。

必要なのは、別のOrderLine全体を返すことです。以下が正しい実装です。

let addLine orderLine1 orderLine2 =
    {
    ProductCode = "TOTAL"
    Qty = orderLine1.Qty + orderLine2.Qty
    Total = orderLine1.Total + orderLine2.Total
    }

これでシグネチャは正しくなりました。addLine : OrderLine -> OrderLine -> OrderLine。

構造全体を返す必要があるため、合計だけでなくProductCodeとQtyも指定する必要があります。 Qtyは簡単で、単に合計すればいいです。ProductCodeについては、文字列”TOTAL”を使うことにしました。実際の製品コードを使うことはできないからです。

少しテストしてみましょう。

// OrderLineを表示するユーティリティメソッド
let printLine {ProductCode=p; Qty=q;Total=t} =
    printfn "%-10s %5i %6g" p q t

let orderLine1 = {ProductCode="AAA"; Qty=2; Total=19.98}
let orderLine2 = {ProductCode="BBB"; Qty=1; Total=1.99}

// 2行を加算して3行目を作成
let orderLine3 = addLine orderLine1 orderLine2
orderLine3 |> printLine // そして表示

結果は以下のようになるはずです。

TOTAL          3  21.97

注：使用されているprintf書式オプションについては、printfに関する投稿を参照してください。

では、これをリストに適用してみましょう。reduceを使います。

let orderLines = [
    {ProductCode="AAA"; Qty=2; Total=19.98}
    {ProductCode="BBB"; Qty=1; Total=1.99}
    {ProductCode="CCC"; Qty=3; Total=3.99}
    ]

orderLines
|> List.reduce addLine
|> printLine

結果：

TOTAL          6  25.96

一見、これは余計な作業に見えるかもしれません。単に合計を求めるだけなのに。しかし、注目してください。合計だけでなく、数量の合計も得られました。

たとえば、printLine関数を再利用して、合計を含むシンプルなレシート印刷関数を簡単に作ることができます。

let printReceipt lines =
    lines
    |> List.iter printLine

    printfn "-----------------------"

    lines
    |> List.reduce addLine
    |> printLine

orderLines
|> printReceipt

これにより、以下のような出力が得られます。

AAA            2  19.98
BBB            1   1.99
CCC            3   3.99
-----------------------
TOTAL          6  25.96

さらに重要なのは、モノイドの増分的な性質を利用して、新しい行が追加されるたびに更新される小計を保持できることです。

以下は例です。

let subtotal = orderLines |> List.reduce addLine
let newLine = {ProductCode="DDD"; Qty=1; Total=29.98}
let newSubtotal = subtotal |> addLine newLine
newSubtotal |> printLine

さらに、++のようなカスタム演算子を定義して、行を数字のように自然に足し合わせることもできます。

let (++) a b = addLine a b  // カスタム演算子

let newSubtotal = subtotal ++ newLine

モノイドパターンを使用すると、全く新しい考え方が開けることがわかります。この「加算」アプローチをほぼあらゆる種類のオブジェクトに適用できます。

たとえば、製品「プラス」製品はどのようになるでしょうか？あるいは、顧客「プラス」顧客は？想像力を働かせてみてください！

まだ終わっていない？

モノイドの3つ目の要件、つまりゼロまたは単位元についてまだ議論していないことにお気づきかもしれません。

この場合、要件は、他の注文行に追加しても元のものが変わらないようなOrderLineが必要だということです。そのようなものはありますか？

現時点ではありません。なぜなら、加算操作は常に製品コードを”TOTAL”に変更するからです。今のところ、私たちが持っているのは実際には半群であり、モノイドではありません。

ご覧のように、半群は完全に使用可能です。しかし、空の行のリストがあって、それらを合計したい場合に問題が生じるでしょう。結果はどうなるべきでしょうか？

一つの回避策は、addLine関数を変更して空の製品コードを無視することです。そして、空のコードを持つ注文行をゼロ要素として使用できます。

以下がその意味するところです。

let addLine orderLine1 orderLine2 =
    match orderLine1.ProductCode, orderLine2.ProductCode with
    // どちらかがゼロの場合？その場合、もう一方を返す
    | "", _ -> orderLine2
    | _, "" -> orderLine1
    // それ以外は以前と同じ
    | _ ->
        {
        ProductCode = "TOTAL"
        Qty = orderLine1.Qty + orderLine2.Qty
        Total = orderLine1.Total + orderLine2.Total
        }

let zero = {ProductCode=""; Qty=0; Total=0.0}
let orderLine1 = {ProductCode="AAA"; Qty=2; Total=19.98}

そして、単位元が期待通りに機能することをテストできます。

assert (orderLine1 = addLine orderLine1 zero)
assert (orderLine1 = addLine zero orderLine1)

これはやや強引に見えるかもしれません。一般的にはこの技術をお勧めしません。単位元を得るためのもう一つの方法があり、それについては後で説明します。

特別な合計型の導入

上記の例では、OrderLine型がとてもシンプルだったため、合計のためにフィールドを流用するのは簡単でした。

しかし、OrderLine型がもっと複雑だったらどうなるでしょうか？たとえば、Priceフィールドも含まれていたら、以下のようになります。

type OrderLine = {
    ProductCode: string
    Qty: int
    Price: float
    Total: float
    }

これで複雑さが増しました。 2つの行を組み合わせるとき、Priceをどう設定すべきでしょうか？平均価格？価格なし？

let addLine orderLine1 orderLine2 =
    {
    ProductCode = "TOTAL"
    Qty = orderLine1.Qty + orderLine2.Qty
    Price = 0 // または平均価格を使う？
    Total = orderLine1.Total + orderLine2.Total
    }

どちらの方法も満足のいくものではありません。

何をすべきかわからないということは、おそらく設計が間違っているということです。

実際、合計には全てのデータではなく、データの一部だけが必要です。これをどのように表現できるでしょうか？

もちろん、判別共用体を使います！一つのケースを製品行に使い、もう一つのケースを合計だけに使います。

以下がその意味するところです。

type ProductLine = {
    ProductCode: string
    Qty: int
    Price: float
    LineTotal: float
    }

type TotalLine = {
    Qty: int
    OrderTotal: float
    }

type OrderLine =
    | Product of ProductLine
    | Total of TotalLine

この設計はずっと良くなりました。合計だけのための特別な構造ができたので、余分なデータを無理に当てはめる必要がなくなりました。ダミーの”TOTAL”製品コードも削除できます。

各レコードで「合計」フィールドの名前を異なるものにしたことに注意してください。このようにフィールド名を一意にすることで、常に型を明示的に指定する必要がなくなります。

残念ながら、加算のロジックはより複雑になりました。全ての組み合わせのケースを扱う必要があります。

let addLine orderLine1 orderLine2 =
    let totalLine =
        match orderLine1,orderLine2 with
        | Product p1, Product p2 ->
            {Qty = p1.Qty + p2.Qty;
            OrderTotal = p1.LineTotal + p2.LineTotal}
        | Product p, Total t ->
            {Qty = p.Qty + t.Qty;
            OrderTotal = p.LineTotal + t.OrderTotal}
        | Total t, Product p ->
            {Qty = p.Qty + t.Qty;
            OrderTotal = p.LineTotal + t.OrderTotal}
        | Total t1, Total t2 ->
            {Qty = t1.Qty + t2.Qty;
            OrderTotal = t1.OrderTotal + t2.OrderTotal}
    Total totalLine // totalLineをラップしてOrderLineを作成

TotalLine値をそのまま返すことはできないことに注意してください。適切なOrderLineを作るには、Totalケースでラップする必要があります。そうしないと、addLineのシグネチャがOrderLine -> OrderLine -> TotalLineになってしまい、正しくありません。 OrderLine -> OrderLine -> OrderLineというシグネチャでなければなりません。他の形は許されません！

2つのケースができたので、printLine関数でも両方を扱う必要があります。

let printLine =  function
    | Product {ProductCode=p; Qty=q; Price=pr; LineTotal=t} ->
        printfn "%-10s %5i @%4g each %6g" p q pr t
    | Total {Qty=q; OrderTotal=t} ->
        printfn "%-10s %5i            %6g" "TOTAL" q t

これで、以前と同じように加算を使えるようになりました。

let orderLine1 = Product {ProductCode="AAA"; Qty=2; Price=9.99; LineTotal=19.98}
let orderLine2 = Product {ProductCode="BBB"; Qty=1; Price=1.99; LineTotal=1.99}
let orderLine3 = addLine orderLine1 orderLine2

orderLine1 |> printLine
orderLine2 |> printLine
orderLine3 |> printLine

単位元の再考

ここでも、単位元の要件を扱っていません。以前と同じトリックを試して、空の製品コードを使うこともできますが、それはProductケースでしか機能しません。

適切な単位元を得るには、共用体型に3つ目のケース、たとえばEmptyOrderを導入する必要があります。

type ProductLine = {
    ProductCode: string
    Qty: int
    Price: float
    LineTotal: float
    }

type TotalLine = {
    Qty: int
    OrderTotal: float
    }

type OrderLine =
    | Product of ProductLine
    | Total of TotalLine
    | EmptyOrder

この追加のケースが利用可能になったので、addLine関数を書き直してこれを扱います。

let addLine orderLine1 orderLine2 =
    match orderLine1,orderLine2 with
    // どちらかがゼロ？その場合、もう一方を返す
    | EmptyOrder, _ -> orderLine2
    | _, EmptyOrder -> orderLine1
    // それ以外は以前と同じ
    | Product p1, Product p2 ->
        Total { Qty = p1.Qty + p2.Qty;
        OrderTotal = p1.LineTotal + p2.LineTotal}
    | Product p, Total t ->
        Total {Qty = p.Qty + t.Qty;
        OrderTotal = p.LineTotal + t.OrderTotal}
    | Total t, Product p ->
        Total {Qty = p.Qty + t.Qty;
        OrderTotal = p.LineTotal + t.OrderTotal}
    | Total t1, Total t2 ->
        Total {Qty = t1.Qty + t2.Qty;
        OrderTotal = t1.OrderTotal + t2.OrderTotal}

これでテストできます。

let zero = EmptyOrder

// 単位元をテスト
let productLine = Product {ProductCode="AAA"; Qty=2; Price=9.99; LineTotal=19.98}
assert (productLine = addLine productLine zero)
assert (productLine = addLine zero productLine)

let totalLine = Total {Qty=2; OrderTotal=19.98}
assert (totalLine = addLine totalLine zero)
assert (totalLine = addLine zero totalLine)

組み込みのList.sum関数の使用

実は、List.sum関数はモノイドについて知っています！加算操作とゼロが何であるかを教えれば、List.foldの代わりにList.sumを直接使うことができます。

これを行うには、型に2つの静的メンバー、+とZeroを付加します。以下のようになります。

type OrderLine with
    static member (+) (x,y) = addLine x y
    static member Zero = EmptyOrder   // プロパティ

これを行えば、List.sumを使用でき、期待通りに機能します。

let lines1 = [productLine]
// 明示的な演算子とゼロを使用したfold
lines1 |> List.fold addLine zero |> printfn "%A"
// 暗黙的な演算子とゼロを使用したsum
lines1 |> List.sum |> printfn "%A"

let emptyList: OrderLine list = []
// 明示的な演算子とゼロを使用したfold
emptyList |> List.fold addLine zero |> printfn "%A"
// 暗黙的な演算子とゼロを使用したsum
emptyList |> List.sum |> printfn "%A"

これが機能するためには、Zeroという名前のメソッドやケースがすでに存在していないことに注意してください。3つ目のケースにZeroという名前を使っていたら、機能しなかったでしょう。

これは巧妙なトリックですが、実際にはComplexNumberやVectorのような本格的な数学関連の型を定義する場合を除いて、良いアイデアだとは思いません。あまりに賢すぎて、明白でないからです。

このトリックを使いたい場合、Zeroメンバーは拡張メソッドではなく、型と一緒に定義する必要があります。

たとえば、以下のコードでは、空の文字列を文字列の「ゼロ」として定義しようとしています。

List.foldは機能します。なぜならString.Zeroがここで拡張メソッドとして見えるからです。しかし、List.sumは失敗します。拡張メソッドが見えないからです。

module StringMonoid =

    // 拡張メソッドを定義
    type System.String with
        static member Zero = ""

    // OK
    ["a";"b";"c"]
    |> List.reduce (+)
    |> printfn "Using reduce: %s"

    // OK。String.Zeroが拡張メソッドとして見える
    ["a";"b";"c"]
    |> List.fold (+) System.String.Zero
    |> printfn "Using fold: %s"

    // エラー。String.ZeroがList.sumに見えない
    ["a";"b";"c"]
    |> List.sum
    |> printfn "Using sum: %s"

異なる構造へのマッピング

共用体に2つの異なるケースを持つことは、注文行の場合は許容できるかもしれませんが、多くの実際のケースでは、このアプローチは複雑すぎたり混乱を招いたりします。

以下のような顧客レコードを考えてみましょう。

open System

type Customer = {
    Name:string // さらに多くの文字列フィールドがあります！
    LastActive:DateTime
    TotalSpend:float }

これらの顧客を2つ「加算」するにはどうすればよいでしょうか？

役立つヒントは、集計が本当に機能するのは数値や類似の型に対してだけだということです。文字列は簡単には集計できません。

そこで、Customerを集計しようとするのではなく、集計可能な情報をすべて含む別のクラスCustomerStatsを定義しましょう。

// 顧客統計を追跡するための型を作成
type CustomerStats = {
    // これらの統計に寄与する顧客数
    Count:int
    // 最後の活動からの日数の合計
    TotalInactiveDays:int
    // 使用金額の合計
    TotalSpend:float }

CustomerStatsのすべてのフィールドは数値なので、2つの統計を加算する方法は明白です。

let add stat1 stat2 = {
    Count = stat1.Count + stat2.Count;
    TotalInactiveDays = stat1.TotalInactiveDays + stat2.TotalInactiveDays
    TotalSpend = stat1.TotalSpend + stat2.TotalSpend
    }

// 中置演算子版も定義
let (++) a b = add a b

いつものように、add関数の入力と出力は同じ型でなければなりません。 CustomerStats -> CustomerStats -> CustomerStatsでなければならず、Customer -> Customer -> CustomerStatsやその他の変形ではいけません。

ここまでは順調です。

では、顧客のコレクションがあり、その集計統計を取得したい場合、どうすればよいでしょうか？

顧客を直接加算することはできないので、まず各顧客をCustomerStatsに変換し、それからモノイド演算を使って統計を加算する必要があります。

以下は例です。

// 顧客を統計に変換
let toStats cust =
    let inactiveDays= DateTime.Now.Subtract(cust.LastActive).Days;
    {Count=1; TotalInactiveDays=inactiveDays; TotalSpend=cust.TotalSpend}

// 顧客のリストを作成
let c1 = {Name="Alice"; LastActive=DateTime(2005,1,1); TotalSpend=100.0}
let c2 = {Name="Bob"; LastActive=DateTime(2010,2,2); TotalSpend=45.0}
let c3 = {Name="Charlie"; LastActive=DateTime(2011,3,3); TotalSpend=42.0}
let customers = [c1;c2;c3]

// 統計を集計
customers
|> List.map toStats
|> List.reduce add
|> printfn "result = %A"

注目すべき点が2つあります。まず、toStatsは1人の顧客の統計を作成します。カウントを1に設定しています。少し奇妙に思えるかもしれませんが、理にかなっています。リストに1人の顧客しかいない場合、それが集計統計になるからです。

2つ目の注目点は、最終的な集計の方法です。まずソース型をモノイドである型に変換するためにmapを使い、次にreduceを使ってすべての統計を集計しています。

う〜ん… mapの後にreduce。聞き覚えがありませんか？

そうです。Googleの有名なMapReduceアルゴリズムは、この概念からインスピレーションを得ています（ただし、詳細は若干異なります）。

先に進む前に、理解度をチェックするための簡単な演習をいくつか紹介します。

CustomerStatsの「ゼロ」は何ですか？空のリストでList.foldを使ってコードをテストしてください。
シンプルなOrderStatsクラスを作成し、この投稿の冒頭で紹介したOrderLine型を集計するために使ってください。

モノイド準同型

これで、モノイド準同型と呼ばれるものを理解するために必要なツールがすべて揃いました。

何を考えているかわかります… うわ！一度に2つの奇妙な数学用語！

しかし、「モノイド」という言葉がもはやそれほど怖くないことを願っています。そして「準同型」は、聞こえるほど複雑ではない数学用語です。ギリシャ語で「同じ形」を意味し、「形」を保つマッピングまたは関数を表します。

実際にはどういう意味でしょうか？

すべてのモノイドには共通の構造があることを見てきました。つまり、基礎となるオブジェクトはかなり異なる場合がある（整数、文字列、リスト、CustomerStatsなど）にもかかわらず、それらの「モノイド性」は同じです。ジョージ・W・ブッシュが言ったように、一度モノイドを見れば、すべてのモノイドを見たことになります。

したがって、モノイド準同型は、「前」と「後」のオブジェクトがかなり異なる場合でも、本質的な「モノイド性」を保つ変換です。

このセクションでは、シンプルなモノイド準同型を見ていきます。これは、モノイド準同型の「Hello World」、「フィボナッチ数列」にあたるもの - 単語数のカウントです。

モノイドとしての文書

テキストブロックを表す型があるとしましょう。以下のようなものです。

type Text = Text of string

もちろん、2つの小さなテキストブロックを加算して、より大きなテキストブロックを作ることができます。

let addText (Text s1) (Text s2) =
    Text (s1 + s2)

加算の動作例は以下の通りです。

let t1 = Text "Hello"
let t2 = Text " World"
let t3 = addText t1 t2

あなたは今や専門家なので、これがモノイドであることをすぐに認識するでしょう。ゼロが明らかにText ""であることも。

さて、本を書いている（この本のような）としましょう。どれだけ書いたかを示す単語数が欲しいとします。

以下は非常に粗い実装と、そのテストです。

let wordCount (Text s) =
    s.Split(' ').Length

// テスト
Text "Hello world"
|> wordCount
|> printfn "The word count is %i"

さて、執筆を続けて、3ページのテキストが出来上がりました。完全な文書の単語数をどのように計算すればよいでしょうか？

一つの方法は、別々のページを加算して完全なテキストブロックを作り、そのテキストブロックにwordCount関数を適用することです。以下は図解です。

ページの加算による単語数カウント

しかし、新しいページを書き終えるたびに、すべてのテキストを加算し、単語数を数え直す必要があります。

疑いなく、もっと良い方法があることがわかるでしょう。すべてのテキストを加算してから数えるのではなく、各ページの単語数を別々に数え、それらの数を加算するのです。以下のようになります。

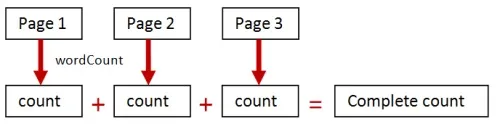
カウントの加算による単語数カウント

2つ目のアプローチは、整数（カウント）自体がモノイドであり、それらを加算して望む結果を得られるという事実に基づいています。

つまり、wordCount関数は「ページ」上の集計を「カウント」上の集計に変換しました。

ここで大きな疑問が生じます。wordCountはモノイド準同型でしょうか？

ページ（テキスト）とカウント（整数）は両方ともモノイドなので、確かに一つのモノイドを別のモノイドに変換しています。

しかし、より微妙な条件は、「形」を保存しているかどうかです。つまり、カウントの加算がページの加算と同じ答えを与えるかどうかです。

この場合、答えはイエスです。したがって、wordCountはモノイド準同型です！

これは明白で、このようなマッピングはすべてモノイド準同型でなければならないと思うかもしれませんが、後でそうでない例を見ていきます。

チャンク化の利点

モノイド準同型アプローチの利点は、「チャンク化可能」であることです。

各マップと単語カウントは他から独立しているため、別々に処理し、後で答えを加算できます。多くのアルゴリズムでは、大きなチャンクよりも小さなチャンクで作業する方が効率的なので、可能な限りこの特性を活用すべきです。

このチャンク化可能性の直接的な結果として、前回の投稿で触れたいくつかの利点が得られます。

まず、増分的です。つまり、最後のページにテキストを追加する際、前のページの単語数を再計算する必要がないため、時間を節約できる可能性があります。

次に、並列化可能です。各チャンクの作業は独立して、異なるコアやマシンで行うことができます。ただし、実際には並列性は過大評価されがちです。小さな部分へのチャンク化が、並列性そのものよりもパフォーマンスに大きな影響を与えます。

単語カウント実装の比較

これで、これら2つの異なる技術を実証するコードを作成する準備が整いました。

まず、上記の基本的な定義から始めましょう。ただし、単語カウントにはsplitの代わりに正規表現を使用します。

module WordCountTest =
    open System

    type Text = Text of string

    let addText (Text s1) (Text s2) =
        Text (s1 + s2)

    let wordCount (Text s) =
        System.Text.RegularExpressions.Regex.Matches(s,@"\S+").Count

次に、1000語を含むページと、1000ページの文書を作成します。

module WordCountTest =

    // 上記のコード

    let page() =
        List.replicate 1000 "hello "
        |> List.reduce (+)
        |> Text

    let document() =
        page() |> List.replicate 1000

実装間で時間差があるかどうかを確認するために、コードの実行時間を計測したいと思います。以下は小さなヘルパー関数です。

module WordCountTest =

    // 上記のコード

    let time f msg =
        let stopwatch = Diagnostics.Stopwatch()
        stopwatch.Start()
        f()
        stopwatch.Stop()
        printfn "Time taken for %s was %ims" msg stopwatch.ElapsedMilliseconds

さて、最初のアプローチを実装しましょう。addTextを使ってすべてのページを加算し、その後、100万語の文書全体に対して単語カウントを行います。

module WordCountTest =

    // 上記のコード

    let wordCountViaAddText() =
        document()
        |> List.reduce addText
        |> wordCount
        |> printfn "The word count is %i"

    time wordCountViaAddText "reduce then count"

2つ目のアプローチでは、まず各ページでwordCountを行い、その後、すべての結果を加算します（もちろんreduceを使用します）。

module WordCountTest =

    // 上記のコード

    let wordCountViaMap() =
        document()
        |> List.map wordCount
        |> List.reduce (+)
        |> printfn "The word count is %i"

    time wordCountViaMap "map then reduce"

コードのわずか2行だけを変更したことに注目してください！

wordCountViaAddTextでは以下のようになっていました。

|> List.reduce addText
|> wordCount

そしてwordCountViaMapでは、基本的にこれらの行を入れ替えました。今度は最初にwordCountを行い、その後にreduceを行います。以下のようになります。

|> List.map wordCount
|> List.reduce (+)

最後に、並列性がどれだけ違いを生むか見てみましょう。List.mapの代わりに組み込みのArray.Parallel.mapを使用します。これは、まずリストを配列に変換する必要があることを意味します。

module WordCountTest =

    // 上記のコード

    let wordCountViaParallelAddCounts() =
        document()
        |> List.toArray
        |> Array.Parallel.map wordCount
        |> Array.reduce (+)
        |> printfn "The word count is %i"

    time wordCountViaParallelAddCounts "parallel map then reduce"

実装を追いかけ、何が起こっているかを理解していただけたと思います。

結果の分析

以下は、私の4コアマシンで実行した異なる実装の結果です。

Time taken for reduce then count was 7955ms
Time taken for map then reduce was 698ms
Time taken for parallel map then reduce was 603ms

これらは粗い結果であり、適切なパフォーマンスプロファイルではないことを認識する必要があります。しかし、それでもmap/reduceバージョンがViaAddTextバージョンの約10倍速いことは非常に明白です。

これがモノイド準同型が重要である理由のカギです - 強力で実装が簡単な「分割統治」戦略を可能にするのです。

はい、使用されているアルゴリズムが非常に非効率的だと主張することもできます。文字列の連結は大きなテキストブロックを蓄積するのに terrible な方法ですし、単語数を数えるもっと良い方法もあります。しかし、これらの注意点があっても、基本的なポイントはまだ有効です：コードのわずか2行を入れ替えることで、大幅なパフォーマンス向上を得られました。

そして、少しのハッシュ化とキャッシュを使えば、増分的な集計の利点も得られます - ページが変更されたときに必要最小限の再計算だけを行います。

この場合、4つのコアすべてを使用したにもかかわらず、並列マップはそれほど大きな違いを生みませんでした。確かに、toArrayで若干のコストを追加しましたが、最良のケースでも、マルチコアマシンでわずかな速度向上しか得られないかもしれません。繰り返しますが、最も大きな違いを生んだのは、map/reduceアプローチに固有の分割統治戦略でした。

モノイド準同型でない例

先ほど、すべてのマッピングが必ずしもモノイド準同型ではないと述べました。このセクションでは、そうでない例を見ていきます。

この例では、単語を数える代わりに、テキストブロック内で最も頻出する単語を返します。

以下が基本的なコードです。

module FrequentWordTest =

    open System
    open System.Text.RegularExpressions

    type Text = Text of string

    let addText (Text s1) (Text s2) =
        Text (s1 + s2)

    let mostFrequentWord (Text s) =
        Regex.Matches(s,@"\S+")
        |> Seq.cast<Match>
        |> Seq.map (fun m -> m.ToString())
        |> Seq.groupBy id
        |> Seq.map (fun (k,v) -> k,Seq.length v)
        |> Seq.sortBy (fun (_,v) -> -v)
        |> Seq.head
        |> fst

mostFrequentWord関数は前のwordCount関数よりも少し複雑なので、ステップバイステップで説明します。

まず、正規表現を使用してすべての非空白文字にマッチします。この結果はMatchのリストではなくMatchCollectionなので、明示的にシーケンス（C#用語ではIEnumerable<Match>）にキャストする必要があります。

次に、各MatchをToString()を使用してマッチした単語に変換します。その後、単語自体でグループ化します。これにより、各ペアが (単語, 単語のリスト)となるペアのリストが得られます。そして、これらのペアを(単語, リストの数)に変換し、降順にソートします（単語数の負の値を使用）。

最後に、最初のペアを取り、そのペアの最初の部分を返します。これが最も頻出する単語です。

では続けて、前回と同様にページと文書を作成しましょう。今回はパフォーマンスに興味がないので、少数のページだけ必要です。しかし、異なるページを作成したいと思います。“hello world”のみを含むページ、“goodbye world”のみを含むページ、そして”foobar”を含む3つ目のページを作成します。（個人的には、あまり面白い本ではないと思います！）

module FrequentWordTest =

    // 上記のコード

    let page1() =
        List.replicate 1000 "hello world "
        |> List.reduce (+)
        |> Text

    let page2() =
        List.replicate 1000 "goodbye world "
        |> List.reduce (+)
        |> Text

    let page3() =
        List.replicate 1000 "foobar "
        |> List.reduce (+)
        |> Text

    let document() =
        [page1(); page2(); page3()]

文書全体に関して、“world”が全体で最も頻出する単語であることは明らかです。

では、前回と同様に2つのアプローチを比較しましょう。最初のアプローチはすべてのページを結合し、その後mostFrequentWordを適用します。以下のようになります。

ページの加算によるmostFrequentWord

2つ目のアプローチは、各ページで別々にmostFrequentWordを行い、その後結果を結合します。以下のようになります。

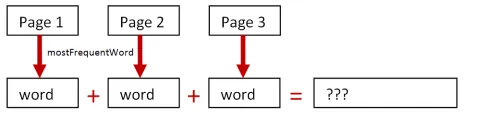
カウントの加算によるmostFrequentWord

以下がコードです。

module FrequentWordTest =

    // 上記のコード

    document()
    |> List.reduce addText
    |> mostFrequentWord
    |> printfn "Using add first, the most frequent word is %s"

    document()
    |> List.map mostFrequentWord
    |> List.reduce (+)
    |> printfn "Using map reduce, the most frequent word is %s"

何が起こったか分かりますか？最初のアプローチは正しい結果を得ました。しかし、2つ目のアプローチは完全に間違った答えを出しました！

Using add first, the most frequent word is world
Using map reduce, the most frequent word is hellogoodbyefoobar

2つ目のアプローチは、各ページの最頻出単語を単に連結しただけです。結果はどのページにも存在しない新しい文字列になりました。完全な失敗です！

何が間違っていたのでしょうか？

文字列は連結下でモノイドですので、このマッピングはモノイド（Text）を別のモノイド（string）に変換しました。

しかし、マッピングは「形」を保存しませんでした。大きなテキストの塊の中で最も頻出する単語は、小さなテキストの塊の中で最も頻出する単語から導き出すことはできません。言い換えれば、これは適切なモノイド準同型ではありません。

モノイド準同型の定義

これら2つの異なる例を再度見て、その違いが何かを理解しましょう。

単語数の例では、ブロックを加算してから単語数を数えても、単語数を数えてから加算しても、同じ最終結果が得られました。以下は図解です。

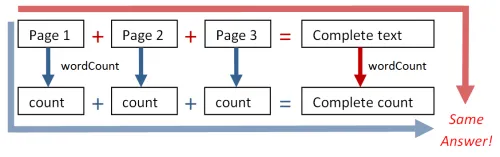
両方の方法による単語数

しかし、最頻出単語の例では、2つの異なるアプローチから同じ答えは得られませんでした。

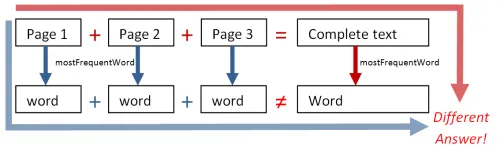
両方の方法による最頻出単語

言い換えれば、wordCountについては以下が成り立ちました。

wordCount(page1) + wordCount(page2) は wordCount(page1 + page2) に等しい

しかし、mostFrequentWordについては以下のようになりました。

mostFrequentWord(page1) + mostFrequentWord(page2) は mostFrequentWord(page1 + page2) に等しくない

これにより、モノイド準同型のより正確な定義が得られます。

あるモノイドから別のモノイドへのマッピング関数（'wordCount'や'mostFrequentWord'のような）が与えられたとき

モノイド準同型であるためには、その関数は以下の要件を満たす必要があります：

function(chunk1) + function(chunk2) は function(chunk1 + chunk2) に等しくなければならない

残念ながら、mostFrequentWordはモノイド準同型ではありません。

つまり、大量のテキストファイルに対してmostFrequentWordを計算したい場合、悲しいことに、まずすべてのテキストを加算する必要があり、分割統治戦略の恩恵を受けることができません。

…本当にそうでしょうか？mostFrequentWordを適切なモノイド準同型に変える方法はないのでしょうか？続きをお楽しみに！

次のステップ

ここまでは、適切なモノイドであるものだけを扱ってきました。しかし、扱いたいものがモノイドでない場合はどうすればよいでしょうか？

このシリーズの次の投稿では、ほぼすべてのものをモノイドに変換するためのヒントをいくつか紹介します。

また、mostFrequentWordの例を修正して適切なモノイド準同型にし、ゼロの厄介な問題を再検討し、それらを作成するためのエレガントなアプローチを紹介します。

その時までお待ちください！

補足文献

データ集計にモノイドを使用することに興味がある場合、以下のリンクに多くの良い議論があります：

TwitterのAlgebirdライブラリ
ほとんどの確率的データ構造はモノイドです。
ガウス分布はモノイドを形成します。
GoogleのMapReduceプログラミングモデル (PDF)。
Monoidify! 効率的なMapReduceアルゴリズムのための設計原則としてのモノイド (PDF)。
LinkedInのHadoop用Hourglassライブラリ
Stack Exchangeより：データベース計算において群、モノイド、環はどのように使われるか？

もう少し技術的な内容を望む場合は、グラフィックス図形をドメインとして使用したモノイドと半群の詳細な研究があります：

モノイド：テーマとバリエーション (PDF)。