数学的関数
関数型プログラミングの原動力は数学から来ています。数学的関数には優れた特徴がいくつかあり、関数型言語はこれらを現実世界で再現しようとしています。
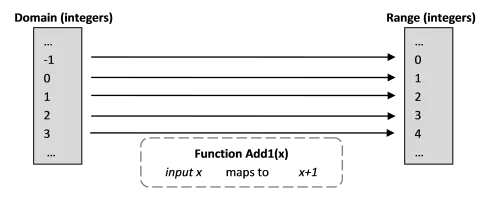
まずは、数に1を足す簡単な数学的関数から見ていきましょう。
Add1(x) = x+1これは何を意味するのでしょうか?一見すると非常に簡単です。ある数から始めて、それに1を足す操作があるということです。
ここで、いくつかの用語を紹介します。
- 定義域:関数の入力として使える値の集合です。この場合、簡単にするために整数だけに限定しましょう。
- 値域:関数の出力値として可能な値の集合です(正確には、終域上の像)。この場合も整数の集合です。
- 写像:関数が定義域を値域に対応付けることを指します。
F#では、この定義は次のように表現できます。
let add1 x = x + 1これをF#のインタラクティブウィンドウに入力すると(セミコロン2つを忘れずに)、結果(関数の「シグネチャ」)が表示されます。
val add1 : int -> intこの出力を詳しく見てみましょう。
- 全体の意味は「関数
add1は整数(定義域)を整数(値域)に写像する」ということです。 add1はval(「value」の略)として定義されています。これがどういう意味か、後ほど値について説明する際に触れます。- 矢印表記
->は定義域と値域を示します。この場合、定義域と値域の両方がint型です。
なお、型は明示的に指定していませんが、F#コンパイラはこの関数が整数を扱っていると推測しました。この推論は後ほど見るように調整可能です。
数学的関数の主要な特性
Section titled “数学的関数の主要な特性”数学的関数には、手続き型プログラミングで慣れ親しんだ関数とは大きく異なる特性があります。
- 同じ入力値に対して常に同じ出力値を返します
- 副作用がありません
これらの特性は非常に強力な利点をもたらします。そのため、関数型プログラミング言語もその設計でこれらの特性を強制しようとします。それぞれについて詳しく見ていきましょう。
数学的関数は常に同じ入力に対して同じ出力を返す
Section titled “数学的関数は常に同じ入力に対して同じ出力を返す”命令型プログラミングでは、関数が何かを「する」あるいは「計算する」と考えます。一方、数学的関数は計算を行いません。純粋に入力から出力への写像です。実際、関数を定義する別の方法として、すべての写像の集合として単純に定義することもできます。
たとえば、非常に粗い方法ですが、 add1 関数を(C#で)次のように定義できます。
int add1(int input){ switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum }}もちろん、すべての可能な整数に対してケースを用意することはできません。しかし、原理は同じです。まったく計算は行われておらず、単なる参照であることがわかります。
数学的関数には副作用がない
Section titled “数学的関数には副作用がない”数学的関数では、入力と出力は論理的に2つの異なるものであり、どちらもあらかじめ定義されています。関数は入力や出力を変更しません。単に定義域の既存の入力値を値域の既存の出力値に写像するだけです。
つまり、関数を評価しても、入力やその他のものに影響を与えることは絶対にありません。関数の評価は実際には何も計算や操作をしていません。単に洗練された参照にすぎないのです。
この値の「不変性」は微妙ですが非常に重要です。数学をしているとき、足し算をしたら下の数が変わるなんて期待しませんよね!たとえば、
x = 5y = x+1xに1を足すことでxが変更されるとは期待しません。異なる数(y)が返され、xは変更されないままであることを期待します。数学の世界では、整数はすでに変更不可能な集合として存在し、 add1 関数は単にそれらの間の関係を定義するだけです。
純粋関数の力
Section titled “純粋関数の力”再現可能な結果を持ち、副作用のない種類の関数は「純粋関数」と呼ばれます。純粋関数を使うと、いくつかの興味深いことができます。
- 簡単な並列化:たとえば、1から1000までの整数があり、1000個の異なるCPUがあれば、各CPUに対応する整数に対して
add1関数を同時に実行させることができます。その際、それらの間に相互作用が必要ないことが確実にわかっています。ロック、ミューテックス、セマフォなどは必要ありません。 - 遅延評価:関数を遅延評価できます。出力が必要になったときにだけ評価します。今評価しても後で評価しても答えが同じであることが確実にわかります。
- 結果のキャッシュ:特定の入力に対して関数を一度だけ評価すれば十分で、その結果をキャッシュできます。同じ入力は常に同じ出力を与えることがわかっているからです。
- 評価順序の自由:複数の純粋関数がある場合、好きな順序で評価できます。これも最終結果に影響を与えることはありません。
このように、プログラミング言語で純粋関数を作成できれば、すぐに多くの強力なテクニックを手に入れることができます。実際、F#ではこれらすべてのことができます。
- 並列処理の例は、「F# を使う理由」シリーズですでに見ました。
- 関数の遅延評価については、「最適化」シリーズで説明します。
- 関数の結果をキャッシュすることを「メモ化」と呼び、これも「最適化」シリーズで説明します。
- 評価順序を気にしないことで、並行プログラミングがはるかに簡単になり、関数の順序変更やリファクタリング時にバグが発生することもありません。
数学的関数の「一見不便な」特性
Section titled “数学的関数の「一見不便な」特性”数学的関数には、プログラミングで使用する際に一見不便に思える特性もいくつかあります。
- 入力値と出力値は不変
- 関数は常に正確に1つの入力と1つの出力を持つ
これらの特性も関数型プログラミング言語の設計に反映されています。それぞれについて見ていきましょう。
入力値と出力値は不変
不変の値は理論的には良いアイデアのように見えます。しかし、従来の方法で変数に代入できなければ、実際にどうやって作業を進められるのでしょうか?
この疑問に対しては、思うほど大きな問題ではないと保証できます。このシリーズを進めていくうちに、実際にどのように機能するかがわかるでしょう。
数学的関数は常に正確に1つの入力と1つの出力を持つ
図からわかるように、数学的関数には常に正確に1つの入力と1つの出力があります。これは関数型プログラミング言語でも同様です。ただし、最初に使用する際にはそれが明らかではないかもしれません。
これは大きな不便のように見えます。2つ(またはそれ以上)のパラメータを持つ関数なしで、どうやって有用なことができるのでしょうか?
実は、これを解決する方法があります。しかも、F#ではそれが完全に透過的です。この方法は「カリー化」と呼ばれ、近々その専用の投稿で詳しく説明します。
実際、後で発見することになりますが、これらの2つの「一見不便な」特性は、信じられないほど有用です。そして、関数型プログラミングを非常に強力にする重要な部分となるのです。