最近、「解説付きローマ数字カタ」という動画を見ました。 この動画では、Corey HainesがTDDアプローチを用いて、Rubyでアラビア数字からローマ数字への変換カタを実装する方法を紹介しています。

この動画を見て、私は非常にイライラしてしまいました。

Corey Hainesのプログラミング能力を軽視するつもりはありません。実際、多くの人がこの動画を有益だと感じているようです。しかし、私にとっては単に苛立たしいものでした。

この投稿では、なぜ私がイライラしたのか、そしてこのような問題に対する私なりのアプローチを説明したいと思います。

要件はどこにある？

「多くのプログラマーは、コーディングを始める前にプログラムの動作概要さえ書きません。コードを生成しないものは時間の無駄だと考えているのです。」

Leslie Lamport, 「ソフトウェアを家のように作るべき理由」

動画では、標準的なTDDの手法に従って進めています。まず初期の失敗ケース（ゼロの処理）を実装し、それを動作させます。次に「1」を処理するテストケースを追加し、それを動作させる、という具合です。

これが私を最初にイライラさせた点です。要件を十分に理解せずにコードに飛びついているのです。

プログラミングカタの目的は、開発者としてのスキルを練習することです。 しかし私にとって、コーディングスキルはソフトウェア開発者の一側面に過ぎず、必ずしも最重要ではありません。

多くの開発者が練習すべきなのは、顧客のニーズ（つまり要件）を聞き、理解することです。 私たちの目標はコードを書くことではなく、価値を提供することだということを忘れてはいけません。

このケースでは、カタにWikiページがありますが、要件はまだあいまいです。 そのため、これは要件を深く掘り下げ、新しいことを学ぶ絶好の機会だと考えています。

ドメインエキスパートになる

実際、要件をできる限り深く理解することには重要な利点があります。

楽しい。新しいドメインを本当に理解するのは楽しいものです。私は新しいことを学ぶのが好きです。それは開発者であることの特典の一つです。

私だけではありません。Dan Northは「アジャイルの加速」というプレゼンテーションで、ドメインエキスパートと密接に働くことの楽しさを語っています。 そのチームの成功の一因は、開発者がトレーダーと一緒にドメイン（トレーディング）を学んだことでした。そのおかげで、コミュニケーションが容易になり、混乱が最小限に抑えられたのです。

良いデザイン。良いソフトウェアを作るには、モデル化しようとしているドメインについてある程度エキスパートになる必要があると私は信じています。 これはもちろんドメイン駆動設計の考え方ですが、アジャイルプロセスの重要な要素でもあります。つまり、全段階で開発者と密接に協力する「オンサイト顧客」の存在です。

そしてほぼ常に、要件を適切に理解することで、解決策を実装する正しい*方法に導かれます。 深い洞察の欠如を、表面的な反復で補うことはできません。

* もちろん「正しい」方法は実際には存在しません。ただ、間違った方法はたくさんあります。ここでは、極端に複雑で保守不可能ではないという意味です。

良いテスト。要件を理解せずに良いテストを作ることはできません。BDDのようなプロセスでは、これが明確になります。 要件は実際にテストになるような形で書かれるのです。

ローマ数字を理解する

「プロジェクトの開始時、私たちがプロジェクトのほとんどの側面について無知である時期に、利用可能な時間を最も有効に使う方法は、考えつく限りのあらゆる視点から我々の無知を特定し、減らすことを試みることです。」 -- Dan North, 「意図的な発見」

では、これをローマ数字カタにどう適用すればいいでしょうか？コードを1行も書く前に、本当にドメインエキスパートになるべきでしょうか？

私は「はい」と答えます！

些細な問題だとわかっていますし、やりすぎに思えるかもしれません。しかし、これはカタです。すべてのステップを注意深く、意識的に練習すべきなのです。

では、ローマ数字について何がわかるでしょうか？

まず、信頼できる情報源によると、ローマ数字はおそらくタリーマーク（訳注：日本で言う「正の字」）に似たものから始まったようです。

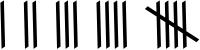
タリーマーク

これは「I」から「IIII」までの単純な線と、「V」の異なる記号を説明しています。

進化するにつれて、10と50、100と500などの記号が追加されました。 1と5で数える方式は、古今の算盤のデザインに見ることができます。

ローマの算盤 現代の算盤

実は、この方式には聞きなれない名前があります。「二・五進法」です。 面白いですね。今後、カジュアルな会話にこのフレーズを盛り込んでみようと思います。 （ちなみに、カウンターとして使用される小石は「calculi」と呼ばれ、高校生の悩みの種（訳注：微積分学）の名前の由来になっています。）

13世紀になって、特定の省略形が追加されました。「IIII」を「IV」に、「VIIII」を「IX」に置き換えるものです。この減算則 により、記号の順序が重要になりました。これは純粋なタリーマークベースのシステムでは必要なかったことです。

これらの新しい要件は、開発業界で何も変わっていないことを示しています...

法王：「減算則をできるだけ早く追加しろ。アラブ人に機能で負けているんだ。」
あなた：「でも陛下、後方互換性がありません。破壊的な変更になります！」
法王：「構わん。来週までに必要だ。」

さて、ローマ数字についてすべて知ったところで、要件を作成するのに十分な情報があるでしょうか？

残念ながら、そうではありません。さらに調査を進めると、一貫性がかなり欠如していることがわかります。ローマ数字にはISOやANSI規格がないのです！

もちろん、これは珍しいことではありません。要件のあいまいさは、ほとんどのソフトウェアプロジェクトに影響します。 実際、開発者としての私たちの仕事の一部は、物事を明確にし、あいまいさを排除することです。では、これまでに知ったことに基づいて要件を作成してみましょう。

このカタの要件

「プログラマーは、その独創性や論理性ではなく、ケース分析の完全性によって評価されるべきである。」 -- Alan Perlis, 警句集

誰もが同意すると思いますが、成功するプロジェクトにするためには、あいまいさがなく、テスト可能な要件を定義することが非常に重要です。

ここで「要件」と言うとき、6ヶ月かけて書く200ページの文書のことを言っているのではありません。 5分か10分で書き下ろせる数個の箇条書きのことを言っているのです。

しかし...要件定義は重要です。コーディングの前に注意深く考えることは、練習する必要がある重要なスキルです。 そのため、どのコードカタでも、この手順を規律の一部として行うことをお勧めします。

では、私が考える要件は次のとおりです。

  • 出力は、1、5、10、50、100、500、1000を集計し、それぞれ「I」、「V」、「X」、「L」、「C」、「D」、「M」の記号を使用して生成します。
  • 記号は降順で書きます：「M」は「D」の前、「D」は「C」の前、「C」は「L」の前、といった具合です。
  • 集計ロジックを使用すると、「I」、「X」、「C」、「M」は最大4回まで、「V」、「L」、「D」は1回だけ繰り返せます。 それ以上になると、複数のタリーマークは次の「上位」のタリーマークに省略します。
  • 最後に、6つの（オプションの）置換規則があります：「IIII」=>「IV」、「VIIII」=>「IX」、「XXXX」=>「XL」、「LXXXX」=>「XC」、「CCCC」=>「CD」、「DCCCC」=>「CM」。これらは降順ルールの例外です。

このリストにはない、もう一つ非常に重要な要件があります。

  • 有効な入力の範囲は何ですか？

これを明記しておかないと、ゼロや負の数も含めたすべての整数が有効だと勘違いしてしまうかもしれません。

では、数百万や数十億といった大きな数字はどうでしょうか？ これらは許可されるのでしょうか？ おそらく許可されないでしょう。

そこで、明示的に有効な入力の範囲を0から4000までとしましょう。では、入力が有効でない場合はどうすべきでしょうか？空の文字列を返すべきでしょうか？例外をスローすべきでしょうか？

F#のような関数型プログラミング言語では、最も一般的なアプローチはOption型を返すか、成功/失敗のChoice型を返すことです。 ここでは単にOptionを使用することにしましょう。要件を完成させるために、以下を追加します。

  • アラビア数字の0は空文字列にマッピングします。
  • 入力が0未満または4000より大きい場合はNoneを返し、それ以外の場合はSome(roman)を返します。ここでromanは上記の説明に従ってアラビア数字をローマ数字に変換したものです。

ここまでのステップをまとめると、ローマ数字について学び、いくつかの面白い発見をし、次の段階のための明確な要件を導き出しました。 これらはすべて、わずか5～10分で完了しました。この時間は、有効に使えたと思います。

テストを書く

「単体テストは、モンスターを探すために暗い部屋に懐中電灯を照らすことに例えられます。 部屋に光を当て、そして全ての怖い隅々まで照らします。 これは部屋にモンスターがいないことを意味するわけではありません。ただ、懐中電灯を照らした場所にモンスターがいないということだけです。」

さて、要件ができたので、テストの作成を始められます。

元の動画では、テストは0から始まり、次に1、というように段階的に開発されていました。

個人的には、このアプローチにはいくつかの問題があると考えています。

まず、TDDの主な目的がテストではなく設計であることを認識すべきです。

しかし、この微視的で段階的な設計アプローチは、特に良い最終結果につながるとは思えません。

たとえば、動画では「I」のケースのテストから「II」のケースのテストに移る際に、実装の複雑さが大きく跳ね上がります。しかし、その理由づけはやや理解しがたく、 自然に前のケースから進化したというよりも、答えをすでに知っている人の手品のようにも感じられます。

残念ながら、厳格なTDDアプローチでは、これがよく起こるのを見てきました。 順調に進んでいるように見えても、突然大きな障害に遭遇し、大規模な再考とリファクタリングが必要になることがあります。

Uncle Bobの変換の優先順位説に従う厳格なTDD実践者なら、それも良いことで、プロセスの一部だと言うでしょう。

個人的には、最も難しい要件から始めて、リスクを前倒しにし、最後まで残さない方が良いと考えます。

第二に、個別のケースをテストするのが好きではありません。テストはできればすべての入力をカバーすべきです。これは常に実現可能というわけではありませんが、このケースのように可能な場合は、そうすべきだと考えます。

2つのテストの比較

これを説明するために、動画で開発されたテストスイートと、より一般的な要件ベースのテストを比較してみましょう。

動画で開発されたテストスイートは、明白な入力と、「念のため」3497のケースのみをチェックします。以下はRubyコードをF#に移植したものです。

[<Test>]
let ``特定の入力に対して、特定の出力を期待する``() = 
    let testpairs = [ 
      (1,"I")
      (2,"II")
      (4,"IV")
      (5,"V")
      (9,"IX")
      (10,"X")
      // 省略
      (900,"CM")
      (1000,"M")
      (3497,"MMMCDXCVII")
      ]
    for (arabic,expectedRoman) in testpairs do
       let roman = arabicToRoman arabic
       Assert.AreEqual(expectedRoman, roman)

この入力セットで、コードが要件を満たしていると、どの程度確信できるでしょうか？

このような単純なケースでは、ある程度確信を持てるかもしれません。 しかし、このテストアプローチは、文書化されていない「魔法の」テスト入力を使用しているため、私には不安があります。

たとえば、なぜ3497という数字が突然選ばれたのでしょうか？それは（a）1000より大きく、（b）4と9を含んでいるからです。 しかし、その選択理由がテストコードに記載されていないのです。

さらに、このテストスイートを要件と比較すると、2番目と3番目の要件が明示的にテストされていないことがわかります。 確かに、3497のテストは暗黙的に順序の要件（「M」が「C」の前、「C」が「X」の前）をチェックしていますが、それが明確に示されているわけではありません。

次に、そのテストと以下のテストを比較してみましょう。

[<Test>]
let ``すべての有効な入力に対して、"I"が最大4回連続することを確認する``() = 
    for i in [1..4000] do
       let roman = arabicToRoman i
       roman |> assertMaxRepetition "I" 4

このテストは、「I」が最大4回しか繰り返せないという要件をチェックしています。

TDDの動画のものとは異なり、このテストケースは1つだけではなく、すべての可能な入力をカバーしています。 このテストがパスすれば、コードがこの特定の要件を完全に満たしていると確信できます。

プロパティベースのテスト

このテストアプローチに馴染みがない方のために説明すると、これは「プロパティベースのテスト」と呼ばれます。 一般的に成り立つべき「プロパティ（特性）」を定義し、そのプロパティが成り立たない場合を見つけるために、可能な限り多くの入力を生成します。

このケースでは、4000個すべての入力をテストできます。 しかし一般的には、問題にはもっと広範囲の入力がありうるため、通常は入力の代表的なサンプルだけをテストします。

ほとんどのプロパティベースのテストツールはHaskellの QuickCheckを参考にしています。 QuickCheckは、エッジケースをできるだけ早く見つけるために、自動的に「興味深い」入力を生成するツールです。 これらの入力には、null、負の数、空のリスト、非ASCII文字を含む文字列などが含まれます。

QuickCheckと同等のものが、F#用のFsCheckを含め、ほとんどの言語で利用可能です。

プロパティベースのテストの利点は、多くの特殊なケースとしてではなく、一般的な観点から要件を考えることを促す点です。

つまり、入力"4"は"IV"にマッピングされるというテストの代わりに、1の位が4の任意の入力は、最後の2文字が"IV"になるというより一般的なテストになります。

プロパティベースのテストの実装

上記の要件に対してプロパティベースのテストに切り替えるには、コードをリファクタリングして （a）プロパティを定義する関数を作成し、（b）そのプロパティを一連の入力に対してチェックします。

以下がリファクタリングしたコードです。

// すべての入力に対して成り立つべきプロパティを定義
let ``最大4つのIを持つ`` arabic = 
   let roman = arabicToRoman arabic
   roman |> assertMaxRepetition "I" 4

// すべての入力を明示的に列挙...
[<Test>]
let ``すべての有効な入力に対して、最大4つの"I"があることを確認``() = 
    for i in [1..4000] do
       //プロパティが成り立つかチェック
       ``最大4つのIを持つ`` i

// ...または FsCheck を使用して入力を生成
let isInRange i = (i >= 1) && (i <= 4000)
// 入力が範囲内であれば、最大4つのIを持つ
let prop i = isInRange i ==> ``最大4つのIを持つ`` i
// このプロパティに対してすべての入力をチェック
Check.Quick prop

または、たとえば40 => "XL"の置換規則をテストしたい場合は、こうします。

// すべての入力に対して成り立つべきプロパティを定義
let ``アラビア数字の10の位が4なら、ローマ数字はXLを1つ持ち、それ以外は持たない`` arabic = 
   let roman = arabicToRoman arabic
   let has4Tens = (arabic % 100 / 10) = 4 
   if has4Tens then
       assertMaxOccurs "XL" 1 roman
   else 
       assertMaxOccurs "XL" 0 roman

// すべての入力を明示的に列挙...
[<Test>]
let ``すべての有効な入力に対して、XLの置換をチェック``() = 
    for i in [1..4000] do
       ``アラビア数字の10の位が4なら、ローマ数字はXLを1つ持ち、それ以外は持たない`` i

// ...または再度 FsCheck を使用して入力を生成
let isInRange i = (i >= 1) && (i <= 4000)
let prop i = isInRange i ==> ``アラビア数字の10の位が4なら、ローマ数字はXLを1つ持ち、それ以外は持たない`` i
Check.Quick prop

プロパティベースのテストについてこれ以上詳しく説明しませんが、手作業で作成した特定の入力を持つケースよりも利点があることがおわかりいただけると思います。

この投稿のコードには、完全なプロパティベースのテストスイートが含まれています。

要件駆動設計？

これで、実装に取り掛かれます。

TDDの動画とは異なり、テストケースではなく要件を反復することで実装を構築したいと思います。 これにはキャッチーなフレーズが必要なので、要件駆動設計（Requirements Driven Design）と呼びましょうか。要件駆動設計マニフェストがもうすぐ登場するかもしれません。

そして、個々の入力を一つずつ処理するコードを実装するのではなく、できるだけ多くの入力ケース（できればすべて）をカバーする実装を好みます。 新しい要件が追加されるたびに、テストを使用して要件をまだ満たしていることを確認しながら、実装を修正または改良します。

しかし、これは動画で示されたTDDとまったく同じではないでしょうか？

いいえ、そうは思いません。TDDのデモンストレーションはテスト駆動でしたが、要件駆動ではありませんでした。1を「I」に、2を「II」にマッピングすることはテストですが、私の見解では真の要件とは言えません。 良い要件はドメインへの洞察に基づいています。2が「II」にマッピングされることをテストするだけでは、その洞察は得られません。

非常にシンプルな実装

他人の実装を批判した後は、自分で実践するか黙るかのどちらかです。

では、私が考えられる最もシンプルな実装は何でしょうか？

アラビア数字をタリーマークに変換するのはどうでしょうか？ 1は「I」に、2は「II」になり、以下同様です。

let arabicToRoman arabic = 
   String.replicate arabic "I"

これを使ってみましょう。

arabicToRoman 1    // "I"
arabicToRoman 5    // "IIIII"
arabicToRoman 10   // "IIIIIIIIII"

このコードは、すでに最初と2番目の要件を満たしています。しかも、すべての入力に対してです！

もちろん、4000個のタリーマークはあまり実用的ではありません。これがローマ人が省略を始めた理由でしょう。

ここでドメインへの洞察が重要になります。タリーマークが省略されていることを理解すれば、コードでそれを再現できます。

では、5つのタリーマークのすべての連続を「V」に変換しましょう。

let arabicToRoman arabic = 
   (String.replicate arabic "I")
    .Replace("IIIII","V")

// テスト
arabicToRoman 1    // "I"
arabicToRoman 5    // "V"
arabicToRoman 6    // "VI"
arabicToRoman 10   // "VV"

しかし今度は「V」の連続が発生します。2つの「V」は「X」に置き換える必要があります。

let arabicToRoman arabic = 
   (String.replicate arabic "I")
    .Replace("IIIII","V")
    .Replace("VV","X")

// テスト
arabicToRoman 1    // "I"
arabicToRoman 5    // "V"
arabicToRoman 6    // "VI"
arabicToRoman 10   // "X" 
arabicToRoman 12   // "XII" 
arabicToRoman 16   // "XVI"

アイデアはおわかりいただけたと思います。省略を追加し続けることができます...

let arabicToRoman arabic = 
   (String.replicate arabic "I")
    .Replace("IIIII","V")
    .Replace("VV","X")
    .Replace("XXXXX","L")
    .Replace("LL","C")
    .Replace("CCCCC","D")
    .Replace("DD","M")

// テスト
arabicToRoman 1    // "I"
arabicToRoman 5    // "V"
arabicToRoman 6    // "VI"
arabicToRoman 10   // "X" 
arabicToRoman 12   // "XII" 
arabicToRoman 16   // "XVI" 
arabicToRoman 3497 // "MMMCCCCLXXXXVII"

これで完成です。最初の3つの要件を満たしました。

4と9を表す省略形を追加したい場合は、最後に、すべての記号を集計した後に追加すればよいでしょう。

let arabicToRoman arabic = 
   (String.replicate arabic "I")
    .Replace("IIIII","V")
    .Replace("VV","X")
    .Replace("XXXXX","L")
    .Replace("LL","C")
    .Replace("CCCCC","D")
    .Replace("DD","M")
    // 省略形の置換
    .Replace("IIII","IV")
    .Replace("VIV","IX")
    .Replace("XXXX","XL")
    .Replace("LXL","XC")
    .Replace("CCCC","CD")
    .Replace("DCD","CM")


// テスト
arabicToRoman 1    // "I"
arabicToRoman 4    // "IV"
arabicToRoman 5    // "V"
arabicToRoman 6    // "VI"
arabicToRoman 10   // "X" 
arabicToRoman 12   // "XII" 
arabicToRoman 16   // "XVI" 
arabicToRoman 40   // "XL" 
arabicToRoman 946  // "CMXLVI" 
arabicToRoman 3497 // "MMMCDXCVII"

このアプローチの優れた点は以下の通りです。

  • 再帰的な設計に直接飛びつくのではなく、ドメインモデル（タリーマーク）の理解から導き出されています。
  • その結果、実装が要件に非常に忠実です。実際、ほぼ自然に書けてしまいます。
  • このステップバイステップのアプローチを見れば、他の人もコードを調べるだけで、その正しさに自信を持てるでしょう。 混乱を招くような再帰や特別なトリックはありません。
  • この実装は、常にすべての入力に対して出力を生成します。中間段階で、すべての要件を満たしていない場合でも、 少なくとも出力（例：10が"VV"にマッピングされる）を生成し、次にすべきことがわかります。

確かに、これは最も効率的なコードとは言えないかもしれません。4000個の"I"を含む文字列を作成しているのですから！ もちろん、より効率的なアプローチは大きなタリーマーク（"M"、次に"D"、次に"C"）を入力から直接引くことで、TDDの動画で示された再帰的な解決策につながります。

しかし一方で、この実装でも十分に効率的かもしれません。 要件にはパフォーマンスの制約について何も書かれていません - YAGNIの原則を思い出しませんか？ - なので、このままでも良いかもしれません。

二・五進法の実装

「二・五進法」という言葉をもう一度使える機会なので、別の実装も紹介したいと思います。

この実装も、ドメインの理解に基づいています。今回は、ローマの算盤です。

算盤では、各行または線が十進法の桁を表します。これは私たちの一般的なアラビア数字表記と同じです。 しかし、その桁の数は、数によって2つの異なる記号で表現できます。

いくつか例を挙げます。

  • 10の位の1は"X"で表します
  • 10の位の2は"XX"で表します
  • 10の位の5は"L"で表します
  • 10の位の6は"LX"で表します

などです。

これは、算盤の玉を文字列表現に変換するアルゴリズムに直接つながります。

  • 入力数を1の位、10の位、100の位、1000の位に分割します。これらは算盤の各行または軸を表します。
  • 各桁の数字を「二・五進法」とその桁に適切な記号を使用して文字列に変換します。
  • 各桁の表現を連結して1つの出力文字列を作成します。

以下は、そのアルゴリズムを直接コードに落とし込んだ実装です。

let biQuinaryDigits place (unit,five) arabic =
    let digit =  arabic % (10*place) / place
    match digit with
    | 0 -> ""
    | 1 -> unit
    | 2 -> unit + unit
    | 3 -> unit + unit + unit
    | 4 -> unit + unit + unit + unit
    | 5 -> five
    | 6 -> five + unit
    | 7 -> five + unit + unit
    | 8 -> five + unit + unit + unit
    | 9 -> five + unit + unit + unit + unit
    | _ -> failwith "0-9のみ想定しています"

let arabicToRoman arabic = 
    let units = biQuinaryDigits 1 ("I","V") arabic
    let tens = biQuinaryDigits 10 ("X","L") arabic
    let hundreds = biQuinaryDigits 100 ("C","D") arabic
    let thousands = biQuinaryDigits 1000 ("M","?") arabic
    thousands + hundreds + tens + units

上記のコードは4と9のケースの省略形を生成しないことに注意してください。 しかし、これは簡単に修正できます。10を表す記号を渡し、4と9のケースの表現を調整するだけです。

let biQuinaryDigits place (unit,five,ten) arabic =
  let digit =  arabic % (10*place) / place
  match digit with
  | 0 -> ""
  | 1 -> unit
  | 2 -> unit + unit
  | 3 -> unit + unit + unit
  | 4 -> unit + five // 5未満に変更 
  | 5 -> five
  | 6 -> five + unit
  | 7 -> five + unit + unit
  | 8 -> five + unit + unit + unit
  | 9 -> unit + ten  // 10未満に変更
  | _ -> failwith "0-9のみ想定しています"

let arabicToRoman arabic = 
  let units = biQuinaryDigits 1 ("I","V","X") arabic
  let tens = biQuinaryDigits 10 ("X","L","C") arabic
  let hundreds = biQuinaryDigits 100 ("C","D","M") arabic
  let thousands = biQuinaryDigits 1000 ("M","?","?") arabic
  thousands + hundreds + tens + units

ここでも、両方の実装は非常にシンプルで検証しやすいです。コードに潜む微妙な例外ケースはありません。

振り返り

この投稿の冒頭で、TDDのデモに苛立ちを感じました。なぜ苛立ったのか、そして私のアプローチがどう異なるかを振り返ってみましょう。

要件

TDDのデモ動画では、要件を文書化する試みが全くありませんでした。 これは危険なことだと私は考えます。特に学習中の場合はなおさらです。

コーディングを始める前に、必ず何をしようとしているのかを明確にする努力をすべきだと私は考えます。

ほんの少しの労力で、後で検証に使える明確な要件を作成しました。

また、有効な入力の範囲も明示的に文書化しました。これは残念ながらTDDのデモには欠けていました。

ドメインの理解

要件が明確に示されている場合でも、作業しているドメインを十分に理解するために時間を使うことは常に価値があると思います。

この場合、ローマ数字がタリーマークベースのシステムだったことを理解することが、後のデザインに役立ちました。（それに、「二・五進法」の意味を学び、この投稿で使用できました！）

ユニットテスト

TDDのデモでは、ユニットテストが一度に1つのケースずつ構築されていました。最初はゼロ、次に1、というように。

上述の通り、このアプローチには非常に不安を感じます。なぜなら（a）良いデザインにつながるとは思えず、（b）単一のケースではすべての可能な入力をカバーできないからです。

要件に直接対応するテストを書くことを強くお勧めします。要件が十分に良ければ、これは一度に多くの入力をカバーすることになり、 できるだけ多くの入力をテストできます。

理想的には、QuickCheckのようなプロパティベースのテストツールを使用します。このアプローチの実装がはるかに簡単になるだけでなく、 設計のプロパティが何であるべきかを特定することを促し、それによってあいまいな要件を明確にするのに役立ちます。

実装

最後に、TDDの動画で示された再帰的な実装とは全く異なる2つの実装を説明しました。

両方の設計は、ドメインの理解から直接導き出されました。最初はタリーマークの使用から、2番目は算盤の使用からです。

私にとって、これらの設計はより理解しやすく（再帰も使わないので）、より信頼しやすいと感じました。

まとめ

（以下のコメントに基づいて追加）

TDDには全く問題がないことを明確にしておきます。カタにも問題はありません。

しかし、このような「飛び込み型」のデモについて私が懸念しているのは、初心者や学習者が無意識のうちに以下のような（暗黙の）教訓を学んでしまう可能性があることです。

  • 質問せずに与えられた要件をそのまま受け入れてもよい。
  • 明確な目標なしに作業してもよい。
  • すぐにコーディングを始めてもよい。
  • 非常に具体的なテスト（例：マジックナンバーを使用）を作成してもよい。
  • 正常系のみを考慮してもよい。
  • 全体像を見ずに細かなリファクタリングを行ってもよい。

個人的には、プロフェッショナルな開発者になるための練習をしているのであれば、以下のことを練習すべきだと思います。

  • コーディングを始める前に、できるだけ多くの情報を求める練習をする。
  • テスト可能な方法で要件を書く練習をする（不明確な入力から）。
  • すぐにコーディングするのではなく、考える（分析と設計）練習をする。
  • 具体的なテストではなく、一般的なテストを作成する練習をする。
  • 不正な入力、エッジケース、エラーについて考え、処理する練習をする。
  • シアリングレイヤー（変化速度の異なる層）がどこにあるべきかという直感を養うために、細かなリファクタリングではなく大規模なリファクタリングを練習する。

これらの原則はすべて、TDD（または少なくともTDDの「ロンドン」学派）やプログラミングカタと完全に両立します。矛盾はなく、なぜ議論の的になるのかわかりません。

あなたはどう思いますか？

多くの方がこの投稿に同意しないかもしれません。（礼儀正しい）議論の準備はできています。以下またはRedditでコメントをお願いします。

この投稿の完全なコードを見たい場合は、こちらのgistで利用可能です。 このgistには、両方の実装の完全なプロパティベースのテストも含まれています。

results matching ""

    No results matching ""