電卓のウォークスルー: パート 4
この一連の記事では、シンプルなポケット電卓アプリを開発しています。
最初の記事では、型ファースト開発を用いて最初の設計を行いました。 そして2番目の記事では、初期実装を作成しました。
前回の記事では、ユーザーインターフェースを含めた残りのコードを作成し、実際に動かしてみました。
しかし、結果は散々なものでした! 問題はコードのバグではなく、コーディングを始める前に要件を十分に検討していなかったことにありました。
まあ、フレッド・ブルックスの有名な言葉にもあるように「捨てるつもりで計画せよ。いずれにせよ捨てることになるのだから」(とはいえ、これは少し単純化しすぎですが)。
幸いなことに、以前の失敗から学び、設計を改善する計画があります。
悪い設計の見直し
Section titled “悪い設計の見直し”設計と実装を見直してみると(このgistを参照)、いくつか気になる点があります。
まず、UpdateDisplayFromDigitなどのイベント処理の型は、電卓の現在の状態、つまりコンテキストを考慮していませんでした。
パッチとして追加したallowAppendフラグは、コンテキストを考慮に入れるための方法の1つでしたが、あまり良い解決策とは言えません。
次に、以下のコードスニペットからわかるように、特定の入力(ZeroとDecimalSeparator)に対して、特別なケースを扱うコードがいくつか存在していました。
let appendCh= match digit with | Zero -> // ディスプレイの先頭に0は1つだけ許可する if display="0" then "" else "0" | One -> "1" | // snip | DecimalSeparator -> if display="" then // 空のディスプレイを特殊なケースで処理する "0" + config.decimalSeparator else if display.Contains(config.decimalSeparator) then // 小数点は2つ許可しない "" else config.decimalSeparatorこれは、これらの入力を実装の詳細の中に隠してしまうのではなく、設計レベルで明確に区別して扱うべきだったことを示唆しています。 設計は、可能な限りそれ自体がドキュメントとしての役割を果たすことが望ましいのです。
有限ステートマシンを設計ツールとして使用する
Section titled “有限ステートマシンを設計ツールとして使用する”行き当たりばったりなアプローチがうまくいかなかった場合、どのように設計を進めていけば良いのでしょうか?
私は、状況に応じて有限ステートマシン (「FSM」――空飛ぶスパゲッティモンスターと混同しないようにしましょう)を使うことを強く推奨しています。 プログラムをステートマシンとしてモデル化できるケースがいかに多いか、きっと驚くことでしょう。
ステートマシンを使うメリットは何でしょうか? 以前の投稿でも触れましたが、改めてその利点を説明します。
各状態は、それぞれ異なる動作を許容します。 言い換えれば、ステートマシンは、コンテキストと、そのコンテキストにおいてどのような操作が可能なのかを明確に意識することを強制します。
今回の電卓の例では、Addが処理された後にコンテキストが変化し、それに伴って数字を累積する際のルールも変わるべきだったのですが、その点を考慮できていませんでした。
すべての状態が明示的に文書化されます。 重要な状態が暗黙的に存在し、ドキュメント化されないままになっていることは、開発現場でよく見られることです。
たとえば、今回の例では、ゼロと小数点を処理するための特別なコードを作成しました。現状では、このコードは実装の中に埋もれてしまっていますが、本来は設計の一部として明示的に示されるべきものです。
ステートマシンは、発生しうるすべての状況を考慮することを強制する設計ツールです。 エラーの一般的な原因として、特定のエッジケースへの対応漏れが挙げられますが、ステートマシンを用いることで、あらゆるケースについて検討するよう促されます。
今回の例では、既に修正したバグ以外にも、数学演算の直後に別の数学演算を行うといった、適切に処理されていないエッジケースがいくつか残っています。 このような場合、電卓はどのように振る舞うべきでしょうか?
F#で単純な有限ステートマシンを実装する方法
Section titled “F#で単純な有限ステートマシンを実装する方法”言語パーサーや正規表現などで使われるような、複雑なFSMをご存知の方も多いでしょう。 これらのステートマシンは、ルールセットや文法から生成されるため、非常に複雑な構造をしています。
しかし、ここで私が取り上げているのは、はるかに単純なステートマシンです。 状態の数が少なく、遷移の数も限られているため、複雑なジェネレーターを使う必要はありません。
具体的にどのようなステートマシンを想定しているのか、以下に例を示します。
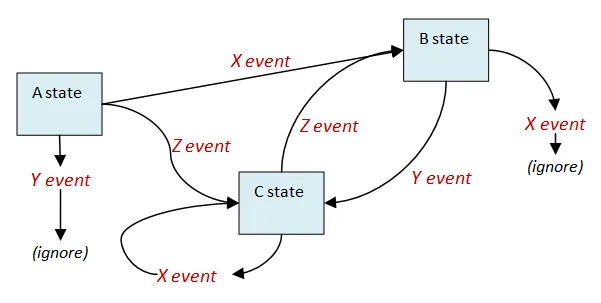
では、F#でこれらの単純なステートマシンを実装する最良の方法は何でしょうか?
FSMの設計と実装は、それ自体が奥深いテーマであり、 NFAとDFA、ムーア型とミーリー型といった独自の用語体系や概念が存在し、 それを専門に扱う企業も存在するほどです。
F#では、テーブル駆動型、相互再帰関数、エージェント、オブジェクト指向スタイルのサブクラスなど、様々な方法でFSMを実装することができます。
しかし、私が好んで用いる方法(特に、アドホックな手動実装を行う場合)は、共用体型とパターンマッチングを積極的に活用する方法です。
まず、すべての状態を表現する共用体型を作成します。 たとえば、「A」、「B」、「C」という3つの状態がある場合、型は次のようになります。
type State = | AState | BState | CState多くの場合、各状態は、その状態に関連するデータを持つことになります。 そのため、これらのデータを保持するための型も定義する必要があります。
type State = | AState of AStateData | BState of BStateData | CStateand AStateData = {something:int}and BStateData = {somethingElse:int}次に、発生する可能性のあるすべてのイベントを、別の共用体型で定義します。イベントがデータを持つ場合は、それも含めます。
type InputEvent = | XEvent | YEvent of YEventData | ZEventand YEventData = {eventData:string}最後に、現在の状態と入力イベントを受け取り、新しい状態を返す「遷移」関数を作成します。
let transition (currentState,inputEvent) = match currentState,inputEvent with | AState, XEvent -> // new state | AState, YEvent -> // new state | AState, ZEvent -> // new state | BState, XEvent -> // new state | BState, YEvent -> // new state | CState, XEvent -> // new state | CState, ZEvent -> // new stateF#のようにパターンマッチングを備えた言語でこのアプローチを採用する利点は、特定の状態とイベントの組み合わせに対応する処理を記述し忘れた場合に、コンパイラが警告を出してくれることです。 これは素晴らしいと思いませんか?
もちろん、状態や入力イベントの数が多いシステムでは、すべての組み合わせを漏れなく処理するのは現実的ではないかもしれません。 しかし、経験上、厄介なバグの多くは、処理すべきでないイベントを処理してしまうことが原因で発生します。これは、最初の設計で、本来は数字を累積すべきでない状態なのに累積してしまっていた問題と全く同じです。
このように、すべての組み合わせを検討するように強制されることは、設計の質を高める上で非常に有効です。
とはいえ、状態とイベントの数が少なくても、組み合わせの数はあっという間に膨大になってしまいます。 そこで、実際にコードを書く際には、以下のように状態ごとにヘルパー関数を用意することで、コードを管理しやすくします。
let aStateHandler stateData inputEvent = match inputEvent with | XEvent -> // new state | YEvent _ -> // new state | ZEvent -> // new state
let bStateHandler stateData inputEvent = match inputEvent with | XEvent -> // new state | YEvent _ -> // new state | ZEvent -> // new state
let cStateHandler inputEvent = match inputEvent with | XEvent -> // new state | YEvent _ -> // new state | ZEvent -> // new state
let transition (currentState,inputEvent) = match currentState with | AState stateData -> // new state aStateHandler stateData inputEvent | BState stateData -> // new state bStateHandler stateData inputEvent | CState -> // new state cStateHandler inputEventでは、このアプローチを試して、上記の状態図を実装してみましょう。
let aStateHandler stateData inputEvent = match inputEvent with | XEvent -> // B状態に遷移する BState {somethingElse=stateData.something} | YEvent _ -> // A状態にとどまる AState stateData | ZEvent -> // C状態に遷移する CState
let bStateHandler stateData inputEvent = match inputEvent with | XEvent -> // B状態にとどまる BState stateData | YEvent _ -> // C状態に遷移する CState
let cStateHandler inputEvent = match inputEvent with | XEvent -> // C状態にとどまる CState | ZEvent -> // B状態に遷移する BState {somethingElse=42}
let transition (currentState,inputEvent) = match currentState with | AState stateData -> aStateHandler stateData inputEvent | BState stateData -> bStateHandler stateData inputEvent | CState -> cStateHandler inputEventこのコードをコンパイルしようとすると、以下のような警告が表示されます。
- (bStateHandler付近)「この式のパターンマッチングが不完全です。たとえば、値 ‘ZEvent’ は、パターンでカバーされていないケースを示している可能性があります。」
- (cStateHandler付近)「この式のパターンマッチングが不完全です。たとえば、値 ‘YEvent (_)’ は、パターンでカバーされていないケースを示している可能性があります。」
これは非常に便利です。いくつかのエッジケースへの対応が漏れており、これらのイベントを処理するようにコードを修正する必要があることを、コンパイラが教えてくれているのです。
ちなみに、ワイルドカードマッチ(アンダースコア)を使ってコードを修正するのは避けましょう! これは、網羅性をチェックするという目的を損なうことになります。 イベントを無視したい場合は、明示的に無視するコードを記述してください。
警告が出ないように修正したコードを以下に示します。
let bStateHandler stateData inputEvent = match inputEvent with | XEvent | ZEvent -> // B状態にとどまる BState stateData | YEvent _ -> // C状態に遷移する CState
let cStateHandler inputEvent = match inputEvent with | XEvent | YEvent _ -> // C状態にとどまる CState | ZEvent -> // B状態に遷移する BState {somethingElse=42}この例のコードは、このgistにあります。
電卓のステートマシンの設計
Section titled “電卓のステートマシンの設計”それでは、電卓のステートマシンを設計していきましょう。まずは、最初のバージョンを以下に示します。
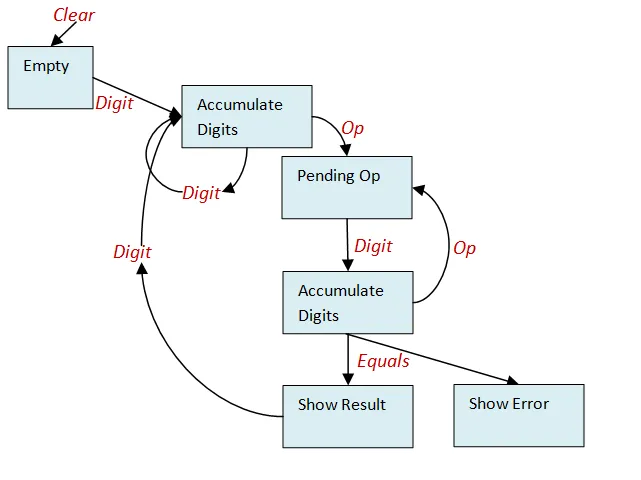
図の中で、各状態はボックスで表され、状態遷移をトリガーするイベント(数字の入力、数学演算、Equalsなど)は赤色で示しています。
たとえば、1、Add、2、Equalsという一連の操作を行うと、図の一番下にある「結果を表示」という状態に遷移することがわかります。
ここで、ゼロと小数点の入力を、設計レベルで特別なイベントとして扱うことを思い出してください。
そこで、これらの入力に対応するイベントと、小数点が連続して入力された場合に2つ目以降を無視する「小数点付き累積」という状態を新たに作成します。
バージョン2を以下に示します。
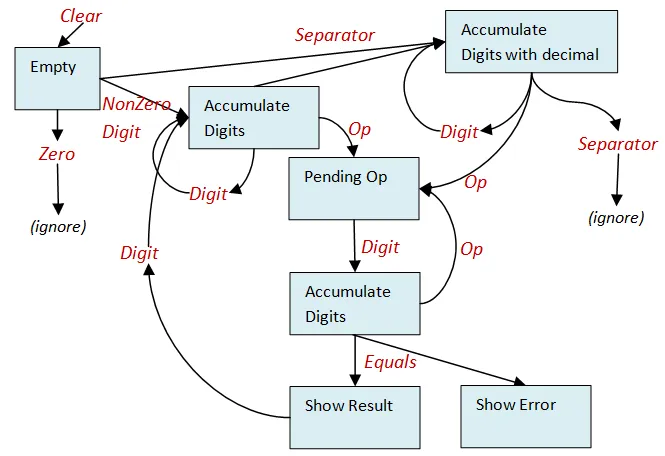
ステートマシンの完成
Section titled “ステートマシンの完成”「優れた芸術家は模倣する。偉大な芸術家は盗む。」 — パブロ・ピカソ(実際にはそうではない)
さて、電卓をモデル化するためにステートマシンを使うことを考えたのは、きっと私だけではないでしょう。
誰か他の人の設計を参考にして、盗む拝借することはできないでしょうか?
そこで、「電卓 ステートマシン」でGoogle検索してみると、こんなものなど、たくさんの検索結果が出てきます。 このページには、詳細な仕様と状態遷移図が載っています。
この図を参考に、さらに検討を重ねた結果、以下の点が明らかになりました。
- 「クリア」状態とゼロ状態は、本質的には同じものです。違いは、保留中の演算があるかどうかだけです。
- 数学演算と
Equalsは、どちらも保留中の計算結果をディスプレイに表示するという点で共通しています。 唯一の違いは、保留中の操作が状態に追加されるかどうかです。 - エラーメッセージのケースは、他の状態とは明確に区別する必要があります。この状態では、
Clear以外の入力はすべて無視されます。
これらの点を踏まえ、状態遷移図のバージョン3を以下に示します。
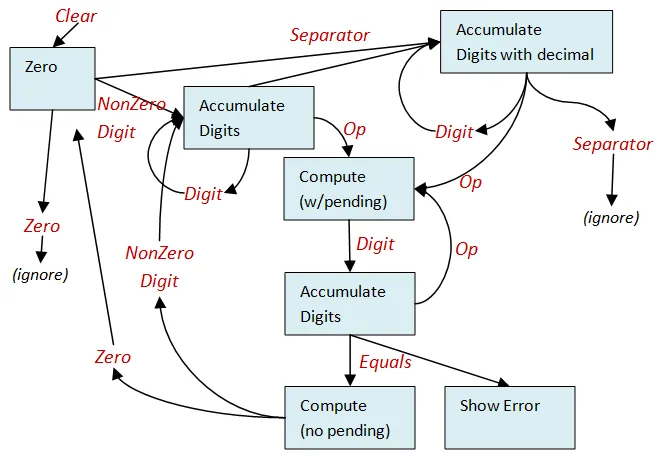
図では、主要な遷移のみを示しています。すべての遷移を表示すると複雑になりすぎるためです。 ただし、詳細な要件を定義するには、これで十分な情報が得られます。
図からわかるように、状態は5つあります。
- ZeroState
- AccumulatorState
- AccumulatorDecimalState
- ComputedState
- ErrorState
入力は6種類あります。
- Zero
- NonZeroDigit
- DecimalSeparator
- MathOp
- Equals
- Clear
それぞれについて、関連付けられるデータがあれば、それも含めて文書化しましょう。
| 状態 | 状態に関連付けられたデータ | 特別な動作? |
|---|---|---|
| ZeroState | (オプション)保留中の操作 | すべてのゼロ入力を無視します |
| AccumulatorState | バッファと(オプション)保留中の操作 | バッファに数字を累積します |
| AccumulatorDecimalState | バッファと(オプション)保留中の操作 | バッファに数字を累積しますが、小数点は無視します |
| ComputedState | 計算された数値と(オプション)保留中の操作 | |
| ErrorState | エラーメッセージ | Clear以外のすべての入力を無視します |
各状態とイベントの組み合わせの文書化
Section titled “各状態とイベントの組み合わせの文書化”次に、各状態とイベントの組み合わせで何が起こるかを検討する必要があります。 上記のサンプルコードと同様に、状態ごとにイベントを処理するだけで済むようにグループ化します。
ZeroState状態から始めましょう。入力の種類ごとの遷移を次に示します。
| 入力 | アクション | 新しい状態 |
|---|---|---|
| Zero | (無視) | ZeroState |
| NonZeroDigit | 数字で新しいアキュムレータを開始します。 | AccumulatorState |
| DecimalSeparator | 「0.」で新しいアキュムレータを開始します。 | AccumulatorDecimalState |
| MathOp | ComputedまたはErrorState状態に移行します。
保留中の操作がある場合は、計算(またはエラー)の結果に基づいてディスプレイを更新します。 また、計算が成功した場合は、現在の数値「0」を使用して、イベントから構築された新しい保留中の操作をプッシュします。 |
ComputedState |
| Equals | MathOpと同様ですが、保留中の操作はありません | ComputedState |
| Clear | (無視) | ZeroState |
AccumulatorState状態でも同じプロセスを繰り返すことができます。入力の種類ごとの遷移を次に示します。
| 入力 | アクション | 新しい状態 |
|---|---|---|
| Zero | バッファに「0」を追加します。 | AccumulatorState |
| NonZeroDigit | バッファに数字を追加します。 | AccumulatorState |
| DecimalSeparator | バッファにセパレータを追加し、新しい状態に遷移します。 | AccumulatorDecimalState |
| MathOp | ComputedまたはErrorState状態に移行します。
保留中の操作がある場合は、計算(またはエラー)の結果に基づいてディスプレイを更新します。 また、計算が成功した場合は、アキュムレータにあるものに基づいて現在の数値を使用して、イベントから構築された新しい保留中の操作をプッシュします。 | ComputedState |
| Equals | MathOpと同様ですが、保留中の操作はありません | ComputedState |
| Clear | ゼロ状態に移行します。保留中の操作をクリアします。 | ZeroState |
AccumulatorDecimalState状態のイベント処理は同じですが、DecimalSeparatorは無視されます。
ComputedState状態はどうでしょうか。入力の種類ごとの遷移を次に示します。
| 入力 | アクション | 新しい状態 |
|---|---|---|
| Zero | ZeroState状態に移行しますが、保留中の操作は保持します | ZeroState |
| NonZeroDigit | 保留中の操作を保持しながら、新しいアキュムレータを開始します | AccumulatorState |
| DecimalSeparator | 保留中の操作を保持しながら、新しい小数アキュムレータを開始します | AccumulatorDecimalState |
| MathOp | Computed状態にとどまります。保留中の操作を、入力イベントから構築された新しい操作に置き換えます | ComputedState |
| Equals | Computed状態にとどまります。保留中の操作をクリアします | ComputedState |
| Clear | ゼロ状態に移行します。保留中の操作をクリアします。 | ZeroState |
最後に、ErrorState状態は非常に簡単です。
| 入力 | アクション | 新しい状態 |
|---|---|---|
| Zero、NonZeroDigit、DecimalSeparator MathOp、Equals |
(無視) | ErrorState |
| Clear | ゼロ状態に移行します。保留中の操作をクリアします。 | ZeroState |
状態をF#コードに変換する
Section titled “状態をF#コードに変換する”ここまで準備を進めてきたので、型への変換は容易です。
主な型を以下に示します。
type Calculate = CalculatorInput * CalculatorState -> CalculatorState// 5つの状態and CalculatorState = | ZeroState of ZeroStateData | AccumulatorState of AccumulatorStateData | AccumulatorWithDecimalState of AccumulatorStateData | ComputedState of ComputedStateData | ErrorState of ErrorStateData// 6つの入力and CalculatorInput = | Zero | Digit of NonZeroDigit | DecimalSeparator | MathOp of CalculatorMathOp | Equals | Clear// 各状態に関連付けられたデータand ZeroStateData = PendingOp optionand AccumulatorStateData = {digits:DigitAccumulator; pendingOp:PendingOp option}and ComputedStateData = {displayNumber:Number; pendingOp:PendingOp option}and ErrorStateData = MathOperationErrorこれらの型を最初の設計(以下)と比較すると、ZeroとDecimalSeparatorが特別な扱いになっていることがわかります。
これは、これらの値が入力型における一級市民に昇格したためです。
// 古い設計からtype CalculatorInput = | Digit of CalculatorDigit | Op of CalculatorMathOp | Action of CalculatorAction
// 新しい設計からtype CalculatorInput = | Zero | Digit of NonZeroDigit | DecimalSeparator | MathOp of CalculatorMathOp | Equals | Clearさらに、古い設計では、すべてのコンテキストのデータを格納する単一の状態型(以下)を使用していましたが、新しい設計では、状態はコンテキストごとに明確に区別されています。
ZeroStateData、AccumulatorStateData、ComputedStateData、ErrorStateDataといった型が定義されていることからも、この違いがはっきりとわかります。
// 古い設計からtype CalculatorState = { display: CalculatorDisplay pendingOp: (CalculatorMathOp * Number) option }
// 新しい設計からtype CalculatorState = | ZeroState of ZeroStateData | AccumulatorState of AccumulatorStateData | AccumulatorWithDecimalState of AccumulatorStateData | ComputedState of ComputedStateData | ErrorState of ErrorStateData新しい設計の基礎ができたので、次はそれに関連する他の型を定義していく必要があります。
and DigitAccumulator = stringand PendingOp = (CalculatorMathOp * Number)and Number = floatand NonZeroDigit= | One | Two | Three | Four | Five | Six | Seven | Eight | Nineand CalculatorMathOp = | Add | Subtract | Multiply | Divideand MathOperationResult = | Success of Number | Failure of MathOperationErrorand MathOperationError = | DivideByZeroそして最後に、サービスを定義します。
// 電卓自体で使用されるサービスtype AccumulateNonZeroDigit = NonZeroDigit * DigitAccumulator -> DigitAccumulatortype AccumulateZero = DigitAccumulator -> DigitAccumulatortype AccumulateSeparator = DigitAccumulator -> DigitAccumulatortype DoMathOperation = CalculatorMathOp * Number * Number -> MathOperationResulttype GetNumberFromAccumulator = AccumulatorStateData -> Number
// UIまたはテストで使用されるサービスtype GetDisplayFromState = CalculatorState -> stringtype GetPendingOpFromState = CalculatorState -> string
type CalculatorServices = { accumulateNonZeroDigit :AccumulateNonZeroDigit accumulateZero :AccumulateZero accumulateSeparator :AccumulateSeparator doMathOperation :DoMathOperation getNumberFromAccumulator :GetNumberFromAccumulator getDisplayFromState :GetDisplayFromState getPendingOpFromState :GetPendingOpFromState }状態を表すデータ構造が複雑になったため、状態から表示テキストを抽出するためのヘルパー関数getDisplayFromStateを追加しました。
この関数は、表示するテキストを取得する必要があるUIや、テストなどの他のクライアントで使用されます。
また、getPendingOpFromStateも追加しました。これにより、UIに保留中の操作を表示できるようになります。
状態ベースの実装の作成
Section titled “状態ベースの実装の作成”それでは、これまで説明してきたパターンを使って、状態ベースの実装を作成していきましょう。
(完全なコードはこのgistから参照できます)。
まずは、状態遷移を行うメイン関数から見ていきましょう。
let createCalculate (services:CalculatorServices) :Calculate = // 部分的に適用されたサービスを使用してローカル関数をいくつか作成する let handleZeroState = handleZeroState services let handleAccumulator = handleAccumulatorState services let handleAccumulatorWithDecimal = handleAccumulatorWithDecimalState services let handleComputed = handleComputedState services let handleError = handleErrorState
fun (input,state) -> match state with | ZeroState stateData -> handleZeroState stateData input | AccumulatorState stateData -> handleAccumulator stateData input | AccumulatorWithDecimalState stateData -> handleAccumulatorWithDecimal stateData input | ComputedState stateData -> handleComputed stateData input | ErrorState stateData -> handleError stateData inputご覧のとおり、責任は多くのハンドラーに渡されます。各状態に1つずつあり、以下で説明します。
しかし、その前に、新しいステートマシンベースの設計と、以前に行った(バグのある!)設計を比較することが有益であると思いました。
以前のコードを次に示します。
let createCalculate (services:CalculatorServices) :Calculate = fun (input,state) -> match input with | Digit d -> let newState = updateDisplayFromDigit services d state newState //return | Op op -> let newState1 = updateDisplayFromPendingOp services state let newState2 = addPendingMathOp services op newState1 newState2 //return | Action Clear -> let newState = services.initState() newState //return | Action Equals -> let newState = updateDisplayFromPendingOp services state newState //return2つの実装を比較すると、イベントよりも状態を重視するようになったことがわかります。 これは、それぞれの実装におけるパターンマッチングの使い方が大きく異なる点に表れています。
- 元のバージョンでは、入力が中心であり、状態はそれに付随するものでした。
- 新しいバージョンでは、状態が中心であり、入力はそれに従属する形になっています。
このように、コンテキストを無視して入力を状態よりも優先させてしまったことが、以前の設計の大きな問題点でした。
先ほども触れましたが、多くの厄介なバグは、本来処理すべきでないタイミングでイベントを処理してしまうことが原因で発生します(以前の設計でまさにその問題が発生しました)。 新しい設計では、最初から状態とコンテキストを重視しているため、以前よりずっと信頼性が高いと感じています。
実際、こうした問題点に気づいているのは私だけではありません。 従来の「イベント駆動型プログラミング」には欠陥があると考える人は多く、 今回のように、より「状態駆動型のアプローチ」 (たとえば、こちらやこちら)を採用することが推奨されています。
ハンドラの作成
Section titled “ハンドラの作成”各状態遷移の要件をすでに文書化したので、コードの作成は簡単です。
ZeroStateハンドラのコードから始めましょう。
let handleZeroState services pendingOp input = // 他の状態に遷移するときに使用される新しいaccumulatorStateDataオブジェクトを作成する let accumulatorStateData = {digits=""; pendingOp=pendingOp} match input with | Zero -> ZeroState pendingOp // ZeroStateにとどまる | Digit digit -> accumulatorStateData |> accumulateNonZeroDigit services digit |> AccumulatorState // AccumulatorStateに遷移する | DecimalSeparator -> accumulatorStateData |> accumulateSeparator services |> AccumulatorWithDecimalState // AccumulatorWithDecimalStateに遷移する | MathOp op -> let nextOp = Some op let newState = getComputationState services accumulatorStateData nextOp newState // ComputedStateまたはErrorStateに遷移する | Equals -> let nextOp = None let newState = getComputationState services accumulatorStateData nextOp newState // ComputedStateまたはErrorStateに遷移する | Clear -> ZeroState None // ZeroStateに遷移し、保留中の操作を破棄する繰り返しますが、本当の作業は、accumulateNonZeroDigitやgetComputationStateなどのヘルパー関数で行われます。これらについては、この後で詳しく見ていきましょう。
AccumulatorStateハンドラのコードを次に示します。
let handleAccumulatorState services stateData input = match input with | Zero -> stateData |> accumulateZero services |> AccumulatorState // AccumulatorStateにとどまる | Digit digit -> stateData |> accumulateNonZeroDigit services digit |> AccumulatorState // AccumulatorStateにとどまる | DecimalSeparator -> stateData |> accumulateSeparator services |> AccumulatorWithDecimalState // AccumulatorWithDecimalStateに遷移する | MathOp op -> let nextOp = Some op let newState = getComputationState services stateData nextOp newState // ComputedStateまたはErrorStateに遷移する | Equals -> let nextOp = None let newState = getComputationState services stateData nextOp newState // ComputedStateまたはErrorStateに遷移する | Clear -> ZeroState None // ZeroStateに遷移し、保留中の操作を破棄するComputedStateハンドラのコードを次に示します。
let handleComputedState services stateData input = let emptyAccumulatorStateData = {digits=""; pendingOp=stateData.pendingOp} match input with | Zero -> ZeroState stateData.pendingOp // 保留中の操作がある場合はZeroStateに遷移する | Digit digit -> emptyAccumulatorStateData |> accumulateNonZeroDigit services digit |> AccumulatorState // AccumulatorStateに遷移する | DecimalSeparator -> emptyAccumulatorStateData |> accumulateSeparator services |> AccumulatorWithDecimalState // AccumulatorWithDecimalStateに遷移する | MathOp op -> // 保留中の操作がある場合は置き換える let nextOp = Some op replacePendingOp stateData nextOp | Equals -> // 保留中の操作がある場合は置き換える let nextOp = None replacePendingOp stateData nextOp | Clear -> ZeroState None // ZeroStateに遷移し、保留中の操作を破棄するヘルパー関数
Section titled “ヘルパー関数”最後に、ヘルパー関数を見てみましょう。
アキュムレータヘルパーは簡単です。適切なサービスを呼び出し、結果をAccumulatorDataレコードにラップするだけです。
let accumulateNonZeroDigit services digit accumulatorData = let digits = accumulatorData.digits let newDigits = services.accumulateNonZeroDigit (digit,digits) let newAccumulatorData = {accumulatorData with digits=newDigits} newAccumulatorData // returngetComputationStateヘルパーは、かなり複雑な処理を行います。おそらく、このコードベースの中で最も複雑な関数と言えるでしょう。
以前実装したupdateDisplayFromPendingOpと基本的な処理は似ていますが、
いくつか変更が加えられています。
services.getNumberFromAccumulatorコードは、状態ベースのアプローチを採用したことで、エラーが発生しなくなりました。シンプルになりましたね!match result with Success/Failureコードは、返り値として2つの状態のいずれかを返します。ComputedStateまたはErrorStateです。- 保留中の操作がない場合でも、有効な
ComputedStateを返す必要があります。この処理はcomputeStateWithNoPendingOpで行います。
let getComputationState services accumulatorStateData nextOp =
// 指定されたdisplayNumberとnextOpパラメーターから // 新しいComputedStateを作成するヘルパー let getNewState displayNumber = let newPendingOp = nextOp |> Option.map (fun op -> op,displayNumber ) {displayNumber=displayNumber; pendingOp = newPendingOp } |> ComputedState
let currentNumber = services.getNumberFromAccumulator accumulatorStateData
// 保留中の操作がない場合は、currentNumberを使用して新しいComputedStateを作成します let computeStateWithNoPendingOp = getNewState currentNumber
maybe { let! (op,previousNumber) = accumulatorStateData.pendingOp let result = services.doMathOperation(op,previousNumber,currentNumber) let newState = match result with | Success resultNumber -> // 保留中の操作がある場合は、結果を使用して新しいComputedStateを作成します getNewState resultNumber | Failure error -> error |> ErrorState return newState } |> ifNone computeStateWithNoPendingOp最後に、以前の実装には全く含まれていなかった、新しいコードについて説明します。
数学演算が連続して入力された場合の処理についてですが、これは単純に、既存の保留中の操作(もしあれば)を新しい操作(もしあれば)に置き換えるだけです。
let replacePendingOp (computedStateData:ComputedStateData) nextOp = let newPending = maybe { let! existing,displayNumber = computedStateData.pendingOp let! next = nextOp return next,displayNumber } {computedStateData with pendingOp=newPending} |> ComputedStateアプリケーションを完成させるには、これまでと同様の方法でサービスとUIを実装すればよいだけです。
幸運なことに、以前のコードのほとんどをそのまま再利用できます。 大きな変更点は入力イベントの構造化の方法だけで、これはボタンハンドラの作成方法に影響します。
電卓のステートマシンバージョンはこちらから入手できます。
新しいコードを実行してみると、初回から問題なく動作し、以前よりもしっかりとした作りになっていることが実感できるはずです。ステートマシン駆動設計のメリットが改めて証明されましたね!
この設計が気に入って、似たようなものを作ってみたい方のために、練習問題をいくつか用意しました。
- まずは、他の演算を追加してみましょう。
1/xやsqrtみたいな単項演算を実装するには、どこをどう変えればいいでしょうか? - 電卓によっては「戻る」ボタンがあるものもあります。これを実装するにはどうすればいいでしょう?すべてのデータ構造が不変なので、簡単にできるはずです。
- ほとんどの電卓には、値を保存したり呼び出したりできるメモリが1つ付いています。これを実装するには、どこをどう変えればいいでしょう?
- ディスプレイに表示できる文字数が10文字まで、という制限は、今の設計には出てきていません。これを設計に組み込むにはどうすればいいでしょう?
このちょっとした試みが、皆さんにとって何かしら参考になれば幸いです。私自身も、この実験を通して学ぶことがありました。 要件定義を疎かにせず、最初から状態ベースのアプローチを採用することを検討するべきだということです。そうすれば、長い目で見れば時間の節約になるかもしれません。