プロパティベースのテストのプロパティ選択

更新情報: これらの投稿に基づいて、プロパティベースのテストに関する講演を行いました。スライドとビデオはこちら です。

前回の投稿では、プロパティベースのテストの基本と、ランダムなテストを生成することで時間を大幅に節約できることを説明しました。

しかし、よくある問題があります。FsCheckやQuickCheckのようなプロパティベースのテストツールを見ると、誰もが素晴らしいと思うのですが… いざ自分でプロパティを作成しようとすると、「どんなプロパティを使えばいいんだ？何も思いつかない！」という不満が必ず出てきます。

この投稿の目的は、コードに適用できるプロパティを発見するのに役立つ、いくつかの一般的なパターンを紹介することです。

プロパティのカテゴリー

私の経験では、多くのプロパティは、以下に挙げる7つのアプローチのいずれかを使うことで発見できます。

• 「異なるパス、同じ結果」
• 「行って帰って元通り」
• 「変わらないものもある」
• 「変われば変わるほど、元のままだ」
• 「まずは小さな問題を解く」
• 「証明は難しくても、検証は簡単」
• 「テストオラクル」

これは決して包括的なリストではなく、私にとって最も役立ったものです。 他の視点については、マイクロソフトのPEXチームがまとめたパターンのリストをご覧ください。

「異なるパス、同じ結果」

この種のプロパティは、操作を異なる順序で組み合わせても、同じ結果になることを前提としています。 たとえば、下の図では、X を実行してから Y を実行しても、Y を実行してから X を実行しても、同じ結果になります。

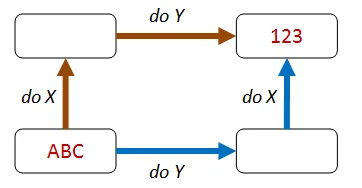
加算の可換性は、このパターンの分かりやすい例です。たとえば、「1を足す」を実行してから「2を足す」を実行した結果は、「2を足す」を実行してから「1を足す」を実行した結果と同じです。

このパターンを一般化すると、広範囲にわたる有用なプロパティを生成できます。この投稿の後半で、このパターンの使い方をさらに紹介します。

「行って帰って元通り」

この種のプロパティは、ある操作とその逆の操作を組み合わせることで、元の値と同じ値になることを前提としています。

下の図では、X を実行すると ABC が何らかのバイナリ形式にシリアル化され、X の逆の操作である何らかのデシリアライズを実行すると、同じ ABC の値が返されます。

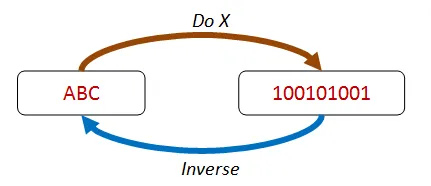
シリアル化/デシリアライズに加えて、addition/subtraction、write/read、setProperty/getProperty など、他の操作のペアもこの方法でチェックできます。

厳密な逆演算ではない場合でも、insert/contains、create/exists などのペアもこのパターンに当てはまります。

「変わらないものもある」

この種のプロパティは、何らかの変換後も保持される不変条件に基づいています。

下の図では、変換によって項目の順序が変わりますが、変換後も同じ4つの項目が存在しています。

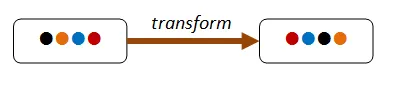
一般的な不変条件には、コレクションのサイズ（たとえば map の場合）、コレクションの内容（たとえば sort の場合）、サイズに比例した高さや深さ（たとえば平衡木）などがあります。

「変われば変わるほど、元のままだ」

この種のプロパティは、「冪等性」に基づいています。つまり、操作を2回行っても、1回行った場合と同じ結果になるということです。

下の図では、distinct を使って集合をフィルタリングすると2つの項目が返されますが、distinct を2回行っても、同じ集合が返されます。

この冪等性という概念は、データベースの更新やメッセージ処理など、様々な場面で役立ちます。

「まずは小さな問題を解く」

この種のプロパティは、「構造帰納法」に基づいています。つまり、大きなものを小さな部分に分解することができ、その小さな部分について何らかのプロパティが真である場合、 大きなものについてもそのプロパティが真であることを証明できることがよくあります。

下の図では、4つの項目からなるリストを、1つの項目と3つの項目からなるリストに分割し、さらにそれを1つの項目と2つの項目からなるリストに分割できることがわかります。 2つの項目からなるリストについてプロパティが成立することが証明できれば、3つの項目からなるリスト、そして4つの項目からなるリストについても成立すると推測できます。

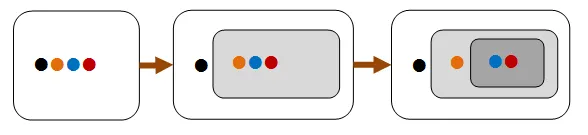
帰納法のプロパティは、リストや木などの再帰的な構造に自然に適用できることがよくあります。

「証明は難しくても、検証は簡単」

結果を求めるアルゴリズムは複雑でも、答えの検証は簡単なことがよくあります。

下の図では、迷路のルートを見つけるのは難しいですが、それが正しいかどうかを確認するのは簡単です。

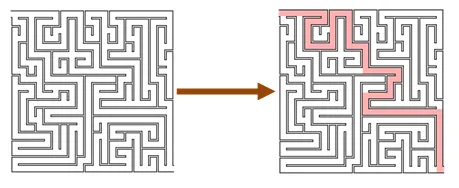
素因数分解など、有名な問題の多くはこの種の問題です。しかし、このアプローチは、単純な問題にも使うことができます。

たとえば、文字列のトークナイザが正しく動作するかどうかを、すべてのトークンを再び連結することで確認できます。結果の文字列は、元の文字列と同じになるはずです。

「テストオラクル」

多くの場合、結果を確認するために使用できる、アルゴリズムまたはプロセスの代替バージョン（「テストオラクル」）があります。

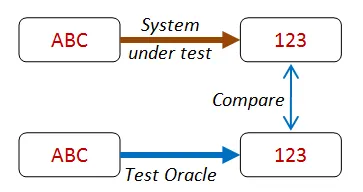
たとえば、最適化の調整を行った高性能なアルゴリズムをテストしたい場合があります。 この場合、はるかに遅いが、正しく書くのがはるかに簡単な、ブルートフォースアルゴリズムと比較することができます。

同様に、並列または並行アルゴリズムの結果を、線形なシングルスレッドバージョンと比較することもできます。

カテゴリーを実際の例で活用する

このセクションでは、これらのカテゴリーを適用して、「リストをソートする」「リストを反転する」などの単純な関数のプロパティを考えられるかどうかを見ていきます。

リストのソートに「異なるパス、同じ結果」を適用する

では、まず「異なるパス、同じ結果」を選び、「リストのソート」関数に適用してみましょう。

List.sortの前に1つの操作を組み合わせ、後に別の操作を組み合わせることで、最終的に同じ結果になるような方法を考えられるでしょうか？ つまり、「上に行ってから上を横切る」のと「下を横切ってから上に行く」のが同じになるようにです。

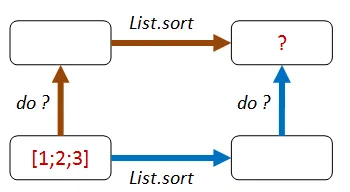
これはどうでしょうか？

• パス1: リストの各要素に1を足してから、ソートします。
• パス2: ソートしてから、リストの各要素に1を足します。
• 両方のリストは等しくなるはずです。

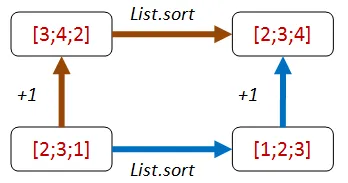
このプロパティを実装したコードを以下に示します。

let ``+1してからソートした結果は、ソートしてから+1した結果と同じである`` sortFn aList =
    let add1 x = x + 1

    let result1 = aList |> sortFn |> List.map add1
    let result2 = aList |> List.map add1 |> sortFn
    result1 = result2

// テスト
let goodSort = List.sort
Check.Quick (``+1してからソートした結果は、ソートしてから+1した結果と同じである`` goodSort)
// OK、100個のテストにパスしました。

さて、これはうまくいきますが、他の多くの変換でもうまくいきます。 たとえば、List.sort を単なる恒等関数として実装した場合でも、このプロパティは同様に成立します。これは自分でテストできます。

let badSort aList = aList
Check.Quick (``+1してからソートした結果は、ソートしてから+1した結果と同じである`` badSort)
// OK、100個のテストにパスしました。

このプロパティの問題点は、「ソート済みであること」を全く活用していないことです。ソートはおそらくリストの順序を変更するでしょうし、確かに最小の要素が最初に来るはずです。

確実にソート後にリストの先頭に来る項目を追加するのはどうでしょうか？

• パス1: リストの末尾に Int32.MinValue を追加してから、ソートします。
• パス2: ソートしてから、リストの先頭に Int32.MinValue を追加します。
• 両方のリストは等しくなるはずです。

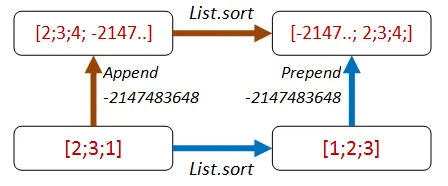
コードは以下の通りです。

let ``最小値を追加してからソートした結果は、ソートしてから最小値を先頭に追加した結果と同じである`` sortFn aList =
    let minValue = Int32.MinValue

    let appendThenSort = (aList @ [minValue]) |> sortFn
    let sortThenPrepend = minValue :: (aList |> sortFn)
    appendThenSort = sortThenPrepend

// テスト
Check.Quick (``最小値を追加してからソートした結果は、ソートしてから最小値を先頭に追加した結果と同じである`` goodSort)
// OK、100個のテストにパスしました。

悪い実装は今度は失敗します。

Check.Quick (``最小値を追加してからソートした結果は、ソートしてから最小値を先頭に追加した結果と同じである`` badSort)
// 反証可能、1回のテスト（2回の縮小）後
// [0]

つまり、[0; minValue] の不正なソートは [minValue; 0] とは同じではないということです。

これは良い結果ですね。

しかし…油断は禁物です。このコードにはハードコードされた値があるので、「最悪なエンタープライズ開発者（EDFH）」（前回の投稿を参照）のつけ込む隙があります。 EDFHは、私たちが常に Int32.MinValue を使用し、常にテストリストの先頭または末尾に追加しているという事実を突いてくるでしょう。

言い換えれば、EDFHは私たちがどちらのパスにいるのかを把握し、それぞれの場合に特化した処理を組み込む可能性があるのです。

// 最悪なエンタープライズ開発者が再び襲来
let badSort2 aList =
    match aList with
    | [] -> []
    | _ ->
        let last::reversedTail = List.rev aList
        if (last = Int32.MinValue) then
            // 最小値が最後にある場合は、先頭に移動する
            let unreversedTail = List.rev reversedTail
            last :: unreversedTail
        else
            aList // そのままにする

そこで、この関数をテストしてみると…

// おやおや、悪い実装がパスしてしまいました。
Check.Quick (``最小値を追加してからソートした結果は、ソートしてから最小値を先頭に追加した結果と同じである`` badSort2)
// OK、100個のテストにパスしました。

これを修正するには、(a) リスト内のどの数値よりも小さい乱数を生成し、(b) 常に追加するのではなく、乱数で決めた位置に挿入します。 しかし、複雑になりすぎるので、ここで一旦立ち止まって考え直してみましょう。

「ソート済みであること」を利用した別の方法として、最初にすべての値の符号を反転し、 ソートの後に符号を反転するパスでは、さらに反転を追加するという方法があります。

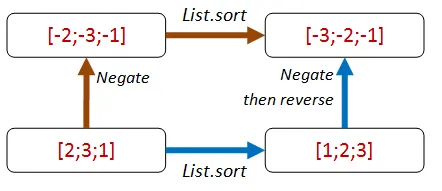
let ``符号を反転してからソートした結果は、ソートしてから符号を反転し、反転した結果と同じである`` sortFn aList =
    let negate x = x * -1

    let negateThenSort = aList |> List.map negate |> sortFn
    let sortThenNegateAndReverse = aList |> sortFn |> List.map negate |> List.rev
    negateThenSort = sortThenNegateAndReverse

このプロパティは、どちらのパスにいるのかを特定するのに役立つマジックナンバーがないため、EDFHが打ち負かすのは困難です。

// テスト
Check.Quick ( ``符号を反転してからソートした結果は、ソートしてから符号を反転し、反転した結果と同じである`` goodSort)
// OK、100個のテストにパスしました。

// テスト
Check.Quick ( ``符号を反転してからソートした結果は、ソートしてから符号を反転し、反転した結果と同じである``  badSort)
// 反証可能、1回のテスト（1回の縮小）後
// [1; 0]

// テスト
Check.Quick ( ``符号を反転してからソートした結果は、ソートしてから符号を反転し、反転した結果と同じである``  badSort2)
// 反証可能、5回のテスト（3回の縮小）後
// [1; 0]

もしかしたら、これは整数のリストのソートしかテストしていないと考える方がいるかもしれません。 しかし、List.sort 関数はジェネリックであり、整数自体については何も知りません。そのため、このプロパティはソートのコアロジックを確実にテストしていると、私は確信しています。

リストの反転関数に「異なるパス、同じ結果」を適用する

さて、List.sort については十分です。同じ考え方をリストの反転関数に適用してみるのはどうでしょうか？

同じ追加/先頭に追加のトリックを実行できます。

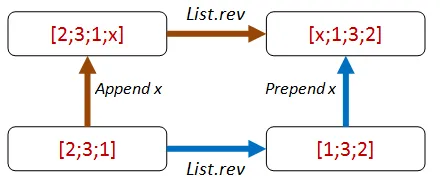
プロパティのコードは以下の通りです。

let ``任意の値を追加してから反転した結果は、反転してから同じ値を先頭に追加した結果と同じである`` revFn anyValue aList =

    let appendThenReverse = (aList @ [anyValue]) |> revFn
    let reverseThenPrepend = anyValue :: (aList |> revFn)
    appendThenReverse = reverseThenPrepend

正しい関数と2つの正しくない関数のテスト結果を以下に示します。

// テスト
let goodReverse = List.rev
Check.Quick (``任意の値を追加してから反転した結果は、反転してから同じ値を先頭に追加した結果と同じである`` goodReverse)
// OK、100個のテストにパスしました。

// 悪い実装は失敗する
let badReverse aList = []
Check.Quick (``任意の値を追加してから反転した結果は、反転してから同じ値を先頭に追加した結果と同じである`` badReverse)
// 反証可能、1回のテスト（2回の縮小）後
// true, []

// 悪い実装は失敗する
let badReverse2 aList = aList
Check.Quick (``任意の値を追加してから反転した結果は、反転してから同じ値を先頭に追加した結果と同じである`` badReverse2)
// 反証可能、1回のテスト（1回の縮小）後
// true, [false]

ここで興味深いことに気づくかもしれません。リストの型を指定していません。このプロパティはどんなリストでも機能します。

このような場合、FsCheckはbool、文字列、整数などのランダムなリストを生成します。

どちらの失敗例でも、anyValue はboolです。つまり、FsCheckは最初にboolのリストを使用しています。

それでは、練習問題です。このプロパティは十分でしょうか？ テストをパスするような実装をEDFHが作成する隙はあるでしょうか？

「行って帰って元通り」

複数パスのスタイルのプロパティが利用できない場合や複雑すぎる場合があるので、他のアプローチを見てみましょう。

まずは、逆演算を含むプロパティからです。

もう一度、リストのソートを考えましょう。ソートの逆演算はありますか？うーん、ないですね。なので、ソートは今は飛ばします。

リストの反転はどうでしょうか？ 実は、反転はそれ自体が逆演算なのです。

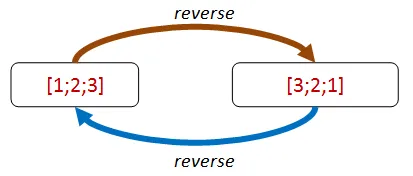
これをプロパティにしてみましょう。

let ``反転してから反転した結果は、元と同じである`` revFn aList =
    let reverseThenReverse = aList |> revFn |> revFn
    reverseThenReverse = aList

そして、パスします。

let goodReverse = List.rev
Check.Quick (``反転してから反転した結果は、元と同じである`` goodReverse)
// OK、100個のテストにパスしました。

しかし、残念ながら、このプロパティでは、誤った実装でもテストをパスしてしまう可能性があります。

let badReverse aList = aList
Check.Quick (``反転してから反転した結果は、元と同じである`` badReverse)
// OK、100個のテストにパスしました。

それでも、逆演算を含むプロパティを使用することは、 逆関数（デシリアライズなど）が実際に主関数（シリアル化など）を「元に戻す」ことを検証するのに非常に役立ちます。

次の投稿では、これを使った実際の例をいくつか紹介します。

「証明は難しくても、検証は簡単」

ここまでは、操作の最終結果を気にせずにプロパティをテストしてきました。

しかし、実際には最終結果が重要です。

通常、テスト対象の関数を複製しなければ、結果が正しいかどうかを判断することはできません。 しかし、多くの場合、結果が間違っているかどうかはかなり簡単に判断できます。上記の迷路の図では、パスが機能するかどうかを簡単に確認できます。

最短パスを探している場合は、それを確認できないかもしれませんが、少なくとも有効なパスがあることはわかります。

この原則は非常に一般的に適用できます。

たとえば、文字列の分割関数が機能しているかどうかを確認したいとします。トークナイザを書く必要はありません。 トークンを連結すると元の文字列に戻ることだけを確認すればよいのです。

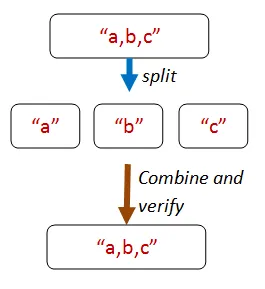
このプロパティのコアコードは以下の通りです。

let concatWithComma s t = s + "," + t

let tokens = originalString.Split [| ',' |]
let recombinedString =
    // 常に少なくとも1つのトークンがあるので、reduceを安全に使用できる
    tokens |> Array.reduce concatWithComma

// 結果を元のものと比較する
originalString = recombinedString

しかし、どのようにして元の文字列を作成すればよいのでしょうか？FsCheckによって生成されたランダムな文字列には、カンマがほとんど含まれていない可能性があります。

FsCheckがランダムデータを生成する方法を正確に制御する方法がありますが、それについては後で説明します。

ここでは、トリックを使います。そのトリックとは、FsCheckにランダムな文字列のリストを生成させ、それらを連結して originalString を構築するというものです。

このプロパティの完全なコードは以下の通りです。

let ``カンマで分割された文字列の要素を連結すると、元の文字列が再作成される`` aListOfStrings =
    // 文字列を作成するためのヘルパー
    let addWithComma s t = s + "," + t
    let originalString = aListOfStrings |> List.fold addWithComma ""

    // プロパティ
    let tokens = originalString.Split [| ',' |]
    let recombinedString =
        // 常に少なくとも1つのトークンがあるので、reduceを安全に使用できる
        tokens |> Array.reduce addWithComma

    // 結果を元のものと比較する
    originalString = recombinedString

これをテストすると、満足のいく結果が得られます。

Check.Quick ``カンマで分割された文字列の要素を連結すると、元の文字列が再作成される``
// OK、100個のテストにパスしました。

リストのソートにおける「証明は難しくても、検証は簡単」

では、この原則をソートされたリストにどのように適用すればよいのでしょうか？どのようなプロパティが簡単に検証できるのでしょうか？

最初に思いつくのは、リスト内の隣接要素について、最初の要素が2番目の要素よりも小さくなるということです。

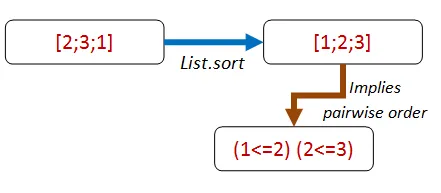
これをプロパティにしてみましょう。

let ``リストの隣接する要素は、順序付けられている`` sortFn aList =
    let pairs = aList |> sortFn |> Seq.pairwise
    pairs |> Seq.forall (fun (x,y) -> x <= y )

しかし、チェックしようとするとおかしなことが起こります。エラーが発生します。

let goodSort = List.sort
Check.Quick (``リストの隣接する要素は、順序付けられている`` goodSort)

System.Exception: Geneflect: type not handled System.IComparable
   at FsCheck.ReflectArbitrary.reflectObj@102-4.Invoke(String message)
   at Microsoft.FSharp.Core.PrintfImpl.go@523-3[b,c,d](String fmt, Int32 len, FSharpFunc`2 outputChar, FSharpFunc`2 outa, b os, FSharpFunc`2 finalize, FSharpList`1 args, Int32 i)
   at Microsoft.FSharp.Core.PrintfImpl.run@521[b,c,d](FSharpFunc`2 initialize, String fmt, Int32 len, FSharpList`1 args)

System.Exception: type not handled System.IComparable はどういう意味でしょうか？これは、FsCheckがランダムなリストを生成しようとしていますが、要素が IComparable 型である必要があることしか理解していないために起こります。 IComparable はインスタンス化できる型ではありません。そのため、FsCheckはエラーを発生させてしまうのです。

これを防ぐにはどうすればよいでしょうか？解決策は、次のように、プロパティに int list などの特定の型を指定することです。

let ``リストの隣接する要素は、順序付けられている`` sortFn (aList:int list) =
    let pairs = aList |> sortFn |> Seq.pairwise
    pairs |> Seq.forall (fun (x,y) -> x <= y )

これで、コードがちゃんと動くようになりました。

let goodSort = List.sort
Check.Quick (``リストの隣接する要素は、順序付けられている`` goodSort)
// OK、100個のテストにパスしました。

プロパティが制約されているにもかかわらず、プロパティは依然として非常に一般的なものであることに注意してください。たとえば、代わりに string list を使用することもでき、同じように動作します。

let ``文字列リストの隣接する要素は、順序付けられている`` sortFn (aList:string list) =
    let pairs = aList |> sortFn |> Seq.pairwise
    pairs |> Seq.forall (fun (x,y) -> x <= y )

Check.Quick (``文字列リストの隣接する要素は、順序付けられている`` goodSort)
// OK、100個のテストにパスしました。

ヒント: FsCheckが「type not handled」をスローする場合は、プロパティに明示的な型制約を追加してください

これで終わりでしょうか？いいえ！このプロパティの問題点の1つは、EDFHによる悪意のある実装を捕捉できないことです。

// 悪い実装がパスする
let badSort aList = []
Check.Quick (``リストの隣接する要素は、順序付けられている`` badSort)
// OK、100個のテストにパスしました。

馬鹿げた実装も動作することに驚きましたか？

うーん。これは、ソートに関連する隣接順序以外のプロパティが見落とされているに違いないということを示しています。何が欠けているのでしょうか？

これは、プロパティベースのテストを行うことで、設計に関する洞察が得られる良い例です。ソートの意味を理解していると思っていましたが、定義をもう少し厳密にする必要に迫られています。

実際には、次の原則を使うことで、この特定の問題を解決します。

「変わらないものもある」

有用な種類のプロパティは、長さや内容を保持するなど、何らかの変換後も保持される不変条件に基づいています。

それらは通常、それ自体では正しい実装を保証するのに十分ではありませんが、より一般的なプロパティに対するカウンターチェックとして機能することがよくあります。

たとえば、前回の投稿では、加算の可換性と結合性を表すプロパティを作成しましたが、単にゼロを返す実装でも同様に成立してしまうことに気づきました。 x + 0 = x をプロパティとして追加して初めて、その特定の悪意のある実装を排除することができました。

そして、上記の「リストのソート」の例では、空のリストを返すだけの関数で「隣接順序」プロパティが成立しました。どうすれば修正できるでしょうか？

最初の試みとして、ソートされたリストの長さを確認するという方法が考えられます。もし長さが異なるならば、ソート関数は明らかに不正を行ったと言えるでしょう。

let ``ソートされたリストの長さは、元と同じである`` sortFn (aList:int list) =
    let sorted = aList |> sortFn
    List.length sorted = List.length aList

チェックしてみると、動作します。

let goodSort = List.sort
Check.Quick (``ソートされたリストの長さは、元と同じである`` goodSort )
// OK、100個のテストにパスしました。

そして、確かに悪い実装は失敗します。

let badSort aList = []
Check.Quick (``ソートされたリストの長さは、元と同じである`` badSort )
// 反証可能、1回のテスト（1回の縮小）後
// [0]

残念ながら、BDFHはまだ諦めていません。なんと、最初の要素をN回繰り返すという、別の抜け道を見つけてしまうのです。

// 悪い実装は同じ長さを持つ
let badSort2 aList =
    match aList with
    | [] -> []
    | head::_ -> List.replicate (List.length aList) head

// たとえば
// badSort2 [1;2;3]  => [1;1;1]

テストすると、パスします。

Check.Quick (``ソートされたリストの長さは、元と同じである`` badSort2)
// OK、100個のテストにパスしました。

さらに、隣接プロパティも成立しています。

Check.Quick (``リストの隣接する要素は、順序付けられている`` badSort2)
// OK、100個のテストにパスしました。

ソートの不変条件 - 2回目の試み

では、もう一度試してみましょう。真の結果 [1;2;3] と偽の結果 [1;1;1] の違いは何でしょうか？

答え: 偽の結果はデータを捨てています。真の結果は常に元のリストと同じ内容を含んでいますが、順序が異なります。

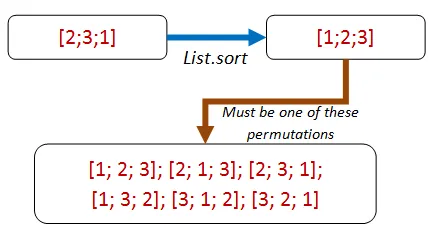
これは新しいプロパティにつながります。ソートされたリストは常に元のリストの順列です。なるほど！では、プロパティを順列で書いてみましょう。

let ``ソートされたリストは、常に元のリストの順列である`` sortFn (aList:int list) =
    let sorted = aList |> sortFn
    let permutationsOfOriginalList = permutations aList

    // ソートされたリストは順列のシーケンスに含まれていなければならない
    permutationsOfOriginalList
    |> Seq.exists (fun permutation -> permutation = sorted)

いいですね。あとは順列関数だけです。

Stack Overflowに行って、盗んで実装を借用してきましょう。以下になります。

/// aListと挿入するanElementが与えられた場合、
/// anElementがaListに挿入された、
/// 可能なすべてのリストを生成する
let rec insertElement anElement aList =
    // https://stackoverflow.com/a/4610704/1136133 より
    seq {
        match aList with
        // 空の場合はシングルトンを返す
        | [] -> yield [anElement]
        // 空でない場合？
        | first::rest ->
            // anElementをリストの先頭に追加して返す
            yield anElement::aList
            // また、すべてのサブリストの先頭にfirstを追加して返す
            for sublist in insertElement anElement rest do
                yield first::sublist
        }

/// リストが与えられた場合、そのすべての順列を返す
let rec permutations aList =
    seq {
        match aList with
        | [] -> yield []
        | first::rest ->
            // 各サブ順列について、
            // firstをどこかに挿入して返す
            for sublist in permutations rest do
                yield! insertElement first sublist
        }

いくつかの簡単な対話型テストで、期待通りに動作することを確認します。

permutations ['a';'b';'c'] |> Seq.toList
//  [['a'; 'b'; 'c']; ['b'; 'a'; 'c']; ['b'; 'c'; 'a']; ['a'; 'c'; 'b'];
//  ['c'; 'a'; 'b']; ['c'; 'b'; 'a']]

permutations ['a';'b';'c';'d'] |> Seq.toList
//  [['a'; 'b'; 'c'; 'd']; ['b'; 'a'; 'c'; 'd']; ['b'; 'c'; 'a'; 'd'];
//   ['b'; 'c'; 'd'; 'a']; ['a'; 'c'; 'b'; 'd']; ['c'; 'a'; 'b'; 'd'];
//   ['c'; 'b'; 'a'; 'd']; ['c'; 'b'; 'd'; 'a']; ['a'; 'c'; 'd'; 'b'];
//   ['c'; 'a'; 'd'; 'b']; ['c'; 'd'; 'a'; 'b']; ['c'; 'd'; 'b'; 'a'];
//   ['a'; 'b'; 'd'; 'c']; ['b'; 'a'; 'd'; 'c']; ['b'; 'd'; 'a'; 'c'];
//   ['b'; 'd'; 'c'; 'a']; ['a'; 'd'; 'b'; 'c']; ['d'; 'a'; 'b'; 'c'];
//   ['d'; 'b'; 'a'; 'c']; ['d'; 'b'; 'c'; 'a']; ['a'; 'd'; 'c'; 'b'];
//   ['d'; 'a'; 'c'; 'b']; ['d'; 'c'; 'a'; 'b']; ['d'; 'c'; 'b'; 'a']]

permutations [3;3] |> Seq.toList
//  [[3; 3]; [3; 3]]

素晴らしい！では、FsCheckを実行してみましょう。

Check.Quick (``ソートされたリストは、常に元のリストの順列である`` goodSort)

うーん。おかしいですね。何も起こっていないようですが、CPUの使用率がなぜか最大になっています。一体何が起きているのでしょうか？

実は、このままでは処理が終わるまで非常に長い時間がかかってしまうのです。もしご自宅で試しているのであれば、今すぐ右クリックして対話型セッションをキャンセルすることをお勧めします。

一見無害に見える permutations は、通常のサイズのリストでは本当に遅いです。 たとえば、わずか10個の項目のリストには3,628,800個の順列があります。20個の項目になると、天文学的な数字になります。

そしてもちろん、FsCheckは何百回もこれらのテストを行うことになります。そのため、重要なヒントがあります。

ヒント: プロパティチェックが非常に高速であることを確認してください。何度も実行することになります。

すでに見てきたように、最良の場合でも、FsCheckはプロパティを100回評価します。そして、縮小が必要な場合は、さらに多くの回数評価を行います。 そのため、テストの実行速度が速いことを確実にする必要があります。

しかし、データベース、ネットワーク、その他の低速な依存関係など、実際のシステムを扱っている場合はどうでしょうか？

QuickCheckの使用に関するビデオ（強くお勧めします）の中で、John Hughesは、 彼のチームがネットワークのパーティションやノードの障害によって引き起こされる可能性のある、分散データストアの欠陥を検出しようとしていたときのことを語っています。

もちろん、実際のノードを何千回も強制終了するのは遅すぎるので、コアロジックを仮想モデルに抽出して、代わりにそれをテストしました。 その結果、この種のテストを容易にするために、コードは後でリファクタリングされました。つまり、プロパティベースのテストは、TDDと同様に、コードの設計に影響を与えたのです。

ソートの不変条件 - 3回目の試み

わかりました。順列をループで処理することはできません。では、同じ考え方を使いますが、この場合に特化した関数、isPermutationOf 関数を記述しましょう。

let ``ソートされたリストは、元のリストと同じ内容を持つ`` sortFn (aList:int list) =
    let sorted = aList |> sortFn
    isPermutationOf aList sorted

     isPermutationOf とその関連ヘルパー関数のコードは以下の通りです。

/// 要素とリスト、および以前にスキップされた他の要素が与えられた場合、
/// 指定された要素を含まない新しいリストを返す。
/// 見つからない場合は、Noneを返す
let rec withoutElementRec anElement aList skipped =
    match aList with
    | [] -> None
    | head::tail when anElement = head ->
        // 一致したので、スキップされたものと残りのものから新しいリストを作成し、
        // それを返す
        let skipped' = List.rev skipped
        Some (skipped' @ tail)
    | head::tail  ->
        // 一致しないので、headをスキップされたものの先頭に追加して再帰する
        let skipped' = head :: skipped
        withoutElementRec anElement tail skipped'

/// 要素とリストが与えられた場合、
/// 指定された要素を含まない新しいリストを返す。
/// 見つからない場合は、Noneを返す
let withoutElement x aList =
    withoutElementRec x aList []

/// 2つのリストが与えられた場合、
/// 順序に関係なく同じ内容であればtrueを返す
let rec isPermutationOf list1 list2 =
    match list1 with
    | [] -> List.isEmpty list2 // 両方とも空の場合はtrue
    | h1::t1 ->
        match withoutElement h1 list2 with
        | None -> false
        | Some t2 ->
            isPermutationOf t1 t2

もう一度テストを実行してみましょう。今回は、宇宙が熱的死を迎える前に完了しました。

Check.Quick (``ソートされたリストは、元のリストと同じ内容を持つ``  goodSort)
// OK、100個のテストにパスしました。

素晴らしいのは、悪意のある実装ではこのプロパティが成立しなくなったことです。

Check.Quick (``ソートされたリストは、元のリストと同じ内容を持つ``  badSort2)
// 反証可能、2回のテスト（5回の縮小）後
// [1; 0]

実際、リストの隣接する要素は、順序付けられている と ソートされたリストは、元のリストと同じ内容を持つ という2つのプロパティがあれば、 実装が正しいことを保証できます。

補足: プロパティの組み合わせ

上で、ソート済みプロパティを定義するには2つのプロパティが必要であることに触れました。 単一のテストができるように、これらを1つのプロパティ ソート済み にまとめることができればよいのですが。

もちろん、2つのコードを1つの関数にマージすることはできますが、関数はできるだけ小さくしておくことが望ましいです。 さらに、同じ内容を持つのようなプロパティは、他のコンテキストでも再利用できる可能性があります。

では、プロパティで動作するように設計された AND と OR に相当するものが必要になります。

FsCheckの出番です。プロパティを組み合わせるための組み込み演算子があります。AND の場合は .&.、OR の場合は .|. です。

使用例を以下に示します。

let ``リストはソート済みである``sortFn (aList:int list) =
    let prop1 = ``リストの隣接する要素は、順序付けられている`` sortFn aList
    let prop2 = ``ソートされたリストは、元のリストと同じ内容を持つ`` sortFn aList
    prop1 .&. prop2

sort の適切な実装で結合されたプロパティをテストすると、すべてが期待通りに動作します。

let goodSort = List.sort
Check.Quick (``リストはソート済みである`` goodSort )
// OK、100個のテストにパスしました。

そして、悪い実装をテストすると、結合されたプロパティも失敗します。

let badSort aList = []
Check.Quick (``リストはソート済みである`` badSort )
// 反証可能、1回のテスト（0回の縮小）後
// [0]

しかし、ここで問題があります。2つのプロパティのどちらが失敗したのでしょうか？

そこで、各プロパティに「ラベル」を追加して、区別できるようにしたいところです。FsCheckでは、これは |@ 演算子を使って行います。

let ``リストはソート済みである（ラベル付き）``sortFn (aList:int list) =
    let prop1 = ``リストの隣接する要素は、順序付けられている`` sortFn aList
                |@ "リストの隣接する要素は、順序付けられている"
    let prop2 = ``ソートされたリストは、元のリストと同じ内容を持つ`` sortFn aList
                |@ "ソートされたリストは、元のリストと同じ内容を持つ"
    prop1 .&. prop2

そして、悪いソートでテストすると、「Label of failing property: ソートされたリストは、元のリストと同じ内容を持つ」というメッセージが表示されます。

Check.Quick (``リストはソート済みである（ラベル付き）`` badSort )
//  反証可能、1回のテスト（2回の縮小）後
//  失敗したプロパティのラベル: ソートされたリストは、元のリストと同じ内容を持つ
//  [0]

これらの演算子の詳細については、FsCheckのドキュメントの「And, Or and Labels」を参照してください。

それでは、プロパティを考案する戦略に戻りましょう。

「小さな問題を解く」

再帰的なデータ構造や再帰的な問題を扱う場合があります。このような場合、より小さな部分で成立するプロパティを見つけることができるでしょう。

たとえば、ソートについて考えてみましょう。次のようなプロパティが考えられます。

リストがソートされているとは、次の場合です。
* 最初の要素が2番目の要素よりも小さい（または等しい）。
* 最初の要素の後の残りの要素もソートされている。

このロジックをコードで表現すると、次のようになります。

let rec ``最初の要素は2番目の要素以下であり、残りの要素もソート済みである`` sortFn (aList:int list) =
    let sortedList = aList |> sortFn
    match sortedList with
    | [] -> true
    | [first] -> true
    | [first;second] ->
        first <= second
    | first::second::tail ->
        first <= second &&
        let subList = second::tail
        ``最初の要素は2番目の要素以下であり、残りの要素もソート済みである`` sortFn subList

このプロパティは、実際のソート関数で成立します。

let goodSort = List.sort
Check.Quick (``最初の要素は2番目の要素以下であり、残りの要素もソート済みである`` goodSort )
// OK、100個のテストにパスしました。

しかし、残念ながら、前の例と同様に、悪意のある実装もパスしてしまいます。

let badSort aList = []
Check.Quick (``最初の要素は2番目の要素以下であり、残りの要素もソート済みである`` badSort )
// OK、100個のテストにパスしました。

let badSort2 aList =
    match aList with
    | [] -> []
    | head::_ -> List.replicate (List.length aList) head

Check.Quick (``最初の要素は2番目の要素以下であり、残りの要素もソート済みである`` badSort2)
// OK、100個のテストにパスしました。

そのため、前と同様に、コードが正しいことを保証するためには、別のプロパティ（同じ内容を持つ 不変条件など）が必要です。

再帰的なデータ構造がある場合は、再帰的なプロパティを探してみてください。コツをつかめば、かなり明白で、簡単に手に入れることができます。

EDFHは本当に問題なのか？

最後のいくつかの例では、些細な、しかし間違った実装でも、良い実装と同じようにプロパティが成立することがよくあることに触れました。

しかし、本当にこれに時間を費やす必要があるのでしょうか？つまり、最初の要素を複製するだけのソートアルゴリズムを実際にリリースした場合、すぐに明らかになるのではないでしょうか？

確かに、本当に悪意のある実装が問題になる可能性は低いでしょう。 一方、プロパティベースのテストはテストプロセスではなく、設計プロセス、つまりシステムが実際に何をしようとしているのかを明確にするのに役立つ手法と考えるべきです。 そして、設計の重要な側面が単純な実装だけで成立する場合、見落としているものがあるのかもしれません。それを発見することで、設計がより明確になり、より堅牢になるでしょう。

「変われば変わるほど、元のままだ」

次のタイプのプロパティは「冪等性」です。冪等性とは、単に何かを2回行っても1回行った場合と同じ結果になることを意味します。 「座ってください」と言ってからもう一度「座ってください」と言っても、2回目の命令は何の効果もありません。

冪等性は、信頼性の高いシステムに不可欠であり、 サービス指向およびメッセージベースのアーキテクチャの重要な側面です。

これらの種類の現実世界のシステムを設計している場合は、要求とプロセスが冪等であることを保証する価値があります。

今はこれ以上詳しく説明しませんが、2つの簡単な例を見てみましょう。

まず、古い友人である sort は冪等ですが（安定性を無視）、reverse は明らかに冪等ではありません。

let ``2回ソートした結果は、1回ソートした結果と同じである`` sortFn (aList:int list) =
    let sortedOnce = aList |> sortFn
    let sortedTwice = aList |> sortFn |> sortFn
    sortedOnce = sortedTwice

// テスト
let goodSort = List.sort
Check.Quick (``2回ソートした結果は、1回ソートした結果と同じである`` goodSort )
// OK、100個のテストにパスしました。

一般に、あらゆる種類のクエリは冪等であるべきです。言い換えれば、「質問をしても答えは変わらない」べきです。

現実の世界では、そうではないかもしれません。データストアに対する単純なクエリを異なる時間に実行すると、異なる結果が得られる可能性があります。

簡単なデモを以下に示します。

まず、クエリごとに異なる結果を返す NonIdempotentService を作成します。

type NonIdempotentService() =
    let mutable data = 0
    member this.Get() =
        data
    member this.Set value =
        data <- value

let ``NonIdempotentServiceを更新後にクエリしても、同じ結果が得られる`` value1 value2 =
    let service = NonIdempotentService()
    service.Set value1

    // 最初のGET
    let get1 = service.Get()

    // 別のタスクがデータストアを更新する
    service.Set value2

    // 最初の時と同じように2回目のGETを呼び出す
    let get2 = service.Get()
    get1 = get2

しかし、今テストしてみると、必要な冪等性プロパティが成立していないことがわかります。

Check.Quick ``NonIdempotentServiceを更新後にクエリしても、同じ結果が得られる``
// 反証可能、2回のテスト後

代わりに、各トランザクションにタイムスタンプを要求する（荒削りな） IdempotentService を作成できます。 この設計では、同じタイムスタンプを使用した複数のGETは、常に同じデータを取得します。

type IdempotentService() =
    let mutable data = Map.empty
    member this.GetAsOf (dt:DateTime) =
        data |> Map.find dt
    member this.SetAsOf (dt:DateTime) value =
        data <- data |> Map.add dt value

let ``IdempotentServiceを更新後にクエリしても、同じ結果が得られる`` value1 value2 =
    let service = IdempotentService()
    let dt1 = DateTime.Now.AddMinutes(-1.0)
    service.SetAsOf dt1 value1

    // 最初のGET
    let get1 = service.GetAsOf dt1

    // 別のタスクがデータストアを更新する
    let dt2 = DateTime.Now
    service.SetAsOf dt2 value2

    // 最初の時と同じように2回目のGETを呼び出す
    let get2 = service.GetAsOf dt1
    get1 = get2

そして、これは動作します。

Check.Quick ``IdempotentServiceを更新後にクエリしても、同じ結果が得られる``
// OK、100個のテストにパスしました。

そのため、REST GETハンドラやデータベースクエリサービスを構築していて、冪等性を確保したい場合は、etag、「as-of」時間、日付範囲などの手法の使用を検討する必要があります。

これを行う方法のヒントが必要な場合は、冪等性パターンを検索すると、いくつかの良い結果が得られます。

「2つの頭脳は1つよりも優れている」

そして最後に、重要なことですが、「テストオラクル」について説明します。テストオラクルとは、単に正しい答えを与える代替実装であり、結果をチェックするために使用できます。

多くの場合、テストオラクルの実装は本番環境には適していません。 遅すぎたり、並列化できなかったり、詩的すぎたりしますが、テストに非常に役立つことに変わりはありません。

「リストのソート」の場合、シンプルだが遅い実装が数多く存在します。たとえば、挿入ソートの簡単な実装を以下に示します。

module InsertionSort =

    // リストをループして、新しい要素をリストに挿入する。
    // より大きな要素が見つかったら、その前に挿入する
    let rec insert newElem list =
        match list with
        | head::tail when newElem > head ->
            head :: insert newElem tail
        | other -> // 空のリストを含む
            newElem :: other

    // リストの残りの部分をソートしてから、
    // 先頭をその中に挿入することでリストをソートする
    let rec sort list =
        match list with
        | []   -> []
        | head::tail ->
            insert head (sort tail)

    // テスト
    // insertionSort  [5;3;2;1;1]

これを用意したら、挿入ソートの結果と比較してテストするプロパティを書くことができます。

let ``ソートの結果は、挿入ソートと同じである`` sortFn (aList:int list) =
    let sorted1 = aList |> sortFn
    let sorted2 = aList |> InsertionSort.sort
    sorted1 = sorted2

良いソートをテストすると、動作します。いいですね。

let goodSort = List.sort
Check.Quick (``ソートの結果は、挿入ソートと同じである`` goodSort)
// OK、100個のテストにパスしました。

そして、悪いソートをテストすると、動作しません。さらにいいですね。

let badSort aList = aList
Check.Quick (``ソートの結果は、挿入ソートと同じである`` badSort)
// 反証可能、4回のテスト（6回の縮小）後
// [1; 0]

2つの異なる方法でローマ数字を生成する

また、どちらの実装が正しいかわからない場合に、2つの異なる実装をクロスチェックするために、テストオラクルアプローチを使用することもできます。

たとえば、私の投稿「「解説付きローマ数字カタ」の解説」では、ローマ数字を生成するための2つの全く異なるアルゴリズムを考え出しました。 これらを互いに比較して、一挙に両方をテストすることはできるでしょうか？

最初のアルゴリズムは、ローマ数字がタリーに基づいていることを理解した上で、次のような単純なコードを作成しました。

let arabicToRomanUsingTallying arabic =
   (String.replicate arabic "I")
    .Replace("IIIII","V")
    .Replace("VV","X")
    .Replace("XXXXX","L")
    .Replace("LL","C")
    .Replace("CCCCC","D")
    .Replace("DD","M")
    // オプションの置換
    .Replace("IIII","IV")
    .Replace("VIV","IX")
    .Replace("XXXX","XL")
    .Replace("LXL","XC")
    .Replace("CCCC","CD")
    .Replace("DCD","CM")

ローマ数字を考える別の方法は、そろばんを想像することです。各軸には4つの「一珠」と1つの「五珠」があります。

これは、いわゆる「バイナリ」アプローチにつながります。

let biQuinaryDigits place (unit,five,ten) arabic =
  let digit =  arabic % (10*place) / place
  match digit with
  | 0 -> ""
  | 1 -> unit
  | 2 -> unit + unit
  | 3 -> unit + unit + unit
  | 4 -> unit + five // 5より1つ少なくなるように変更
  | 5 -> five
  | 6 -> five + unit
  | 7 -> five + unit + unit
  | 8 -> five + unit + unit + unit
  | 9 -> unit + ten  // 10より1つ少なくなるように変更
  | _ -> failwith "Expected 0-9 only"

let arabicToRomanUsingBiQuinary arabic =
  let units = biQuinaryDigits 1 ("I","V","X") arabic
  let tens = biQuinaryDigits 10 ("X","L","C") arabic
  let hundreds = biQuinaryDigits 100 ("C","D","M") arabic
  let thousands = biQuinaryDigits 1000 ("M","?","?") arabic
  thousands + hundreds + tens + units

これで、2つの全く異なるアルゴリズムができました。これらを互いにクロスチェックして、同じ結果が得られるかどうかを確認できます。

let ``バイナリ法とタリー法は、同じ結果を与える`` arabic =
    let tallyResult = arabicToRomanUsingTallying arabic
    let biquinaryResult = arabicToRomanUsingBiQuinary arabic
    tallyResult = biquinaryResult

しかし、このコードを実行しようとすると、String.replicate の呼び出しにより、ArgumentException: The input must be non-negative が発生します。

Check.Quick ``バイナリ法とタリー法は、同じ結果を与える``
// ArgumentException: The input must be non-negative.

そのため、正の入力のみを含める必要があります。また、アルゴリズムがそこで破綻するため、4000より大きい数値も除外する必要があります。

このフィルタはどのように実装すればよいでしょうか？

前回の投稿で、事前条件を使用できることを説明しました。しかし、この例では、別の方法を試して、ジェネレーターを変更してみましょう。

まず、必要なようにフィルタリングされた新しい任意の整数 arabicNumber を定義します （「任意」とは、前回の投稿で説明したように、ジェネレーターアルゴリズムと縮小アルゴリズムの組み合わせです）。

let arabicNumber = Arb.Default.Int32() |> Arb.filter (fun i -> i > 0 && i <= 4000)

次に、Prop.forAll ヘルパーを使用して、「arabicNumber」のみを使用するように制約された新しいプロパティを作成します。

このプロパティには、「arabicNumberのすべての値について、バイナリ法とタリー法は同じ結果を与える」という、かなり巧妙な名前を付けます。

let ``arabicNumberのすべての値について、バイナリ法とタリー法は同じ結果を与える`` =
    Prop.forAll arabicNumber ``biquinary should give same result as tallying``

最後に、クロスチェックテストを実行できます。

Check.Quick ``arabicNumberのすべての値について、バイナリ法とタリー法は同じ結果を与える``
// OK、100個のテストにパスしました。

これでOKです。どちらのアルゴリズムも正しく動作しているようです。

「モデルベース」テスト

後の投稿で詳しく説明する「モデルベース」テストは、テストオラクルのバリエーションです。

その仕組みは、テスト対象の（複雑な）システムと並行して、簡略化されたモデルを作成するというものです。

そして、テスト対象のシステムに何かを行うときは、 モデルにも同じ（ただし簡略化された）ことを行います。

最後に、モデルの状態とテスト対象のシステムの状態を比較します。同じであれば、完了です。そうでない場合は、SUTにバグがあるか、モデルが間違っているため、やり直す必要があります。

幕間: プロパティを見つけるゲーム

これで、さまざまなプロパティのカテゴリーの説明は終わりです。1分ほどで、もう一度すべてを説明します。しかし、その前に、幕間です。

プロパティを見つけようとするのが精神的な挑戦だと感じる場合は、あなただけではありません。ゲームだと思うと役に立つでしょうか？

実は、プロパティベースのテストに基づいたゲームがあります。

それはZendoといいます。 テーブルの上にオブジェクトのセット（プラスチック製のピラミッドなど）を配置し、各レイアウトがパターン、つまりルール、または私たちが今言うようにプロパティに準拠するようにするというものです。

他のプレイヤーは、見えているものに基づいて、ルール（プロパティ）が何であるかを推測する必要があります。

進行中のZendoゲームの写真を以下に示します。

白い石はプロパティが成立していることを意味し、黒い石は失敗を意味します。ここのルールがわかりますか？ 「セットには地面に触れていない黄色のピラミッドがなければならない」のようなものだと思います。

なるほど、Zendoは実際にはプロパティベースのテストからインスピレーションを得たものではありませんが、 楽しいゲームであり、プログラミングカンファレンスに登場することさえあります。

Zendoについてもっと知りたい場合は、ルールはこちらです。

カテゴリーをもう一度適用する

これらのカテゴリーをすべて念頭に置いて、別の問題の例を見て、プロパティを見つけられるかどうかを確認しましょう。

このサンプルは、Kent Beckの著書「テスト駆動開発入門」で説明されている、よく知られた Dollar の例に基づいています。

Growing Object-Oriented Software Guided by Tests で有名なNat Pryceは、 しばらく前にプロパティベースのテストに関するブログ記事（「QuickCheckを使ったテスト駆動開発の探求」）を書きました。

その中で彼は、プロパティベースのテストが実際に役立つことについて、いくつかの不満を表明しました。そこで、彼が参照した例を再検討し、私たちに何ができるかを見てみましょう。

設計自体を批判して、より型駆動型にすることはしません。他の人がそれをやっています。 代わりに、設計をそのまま受け入れて、どのようなプロパティを考え出すことができるかを見てみましょう。

では、何があるのでしょうか？

• Amount を格納する Dollar クラス。
• 明らかな方法で金額を変換するメソッド Add と Times。

// メンバーを持つオブジェクト指向スタイルのクラス
type Dollar(amount:int) =
    member val Amount  = amount with get, set
    member this.Add add =
        this.Amount <- this.Amount + add
    member this.Times multiplier  =
        this.Amount <- this.Amount * multiplier
    static member Create amount  =
        Dollar amount

では、まず対話型で試して、期待通りに動作することを確認しましょう。

let d = Dollar.Create 2
d.Amount  // 2
d.Times 3
d.Amount  // 6
d.Add 1
d.Amount  // 7

しかし、これは単なる遊びであり、本当のテストではありません。では、どのようなプロパティを考え出すことができるでしょうか？

もう一度すべてを検討してみましょう。

• 異なるパス、同じ結果
• 逆演算
• 不変条件
• 冪等性
• 構造帰納法
• 検証は簡単
• テストオラクル

今のところ、「異なるパス」は飛ばしましょう。逆演算はどうでしょうか？使用できる逆演算はありますか？

はい、セッターとゲッターは、プロパティを作成できる逆演算を形成します。

let ``設定してから取得した結果は、同じである`` value =
    let obj = Dollar.Create 0
    obj.Amount <- value
    let newValue = obj.Amount
    value = newValue

Check.Quick ``設定してから取得した結果は、同じである``
// OK、100個のテストにパスしました。

冪等性も関係があります。たとえば、2回連続でセットを行うことは、1回だけ行うことと同じです。 そのためのプロパティを以下に示します。

let ``金額の設定は冪等である`` value =
    let obj = Dollar.Create 0
    obj.Amount <- value
    let afterFirstSet = obj.Amount
    obj.Amount <- value
    let afterSecondSet = obj.Amount
    afterFirstSet = afterSecondSet

Check.Quick ``金額の設定は冪等である``
// OK、100個のテストにパスしました。

「構造帰納法」のプロパティはありますか？ いいえ、このケースには関係ありません。

「検証は簡単」なプロパティはありますか？ 明らかなものはありません。   最後に、テストオラクルはありますか？ いいえ。これも関係ありませんが、実際に複雑な通貨管理システムを設計している場合は、 サードパーティシステムと結果をクロスチェックすると非常に役立つ可能性があります。

不変のDollarのプロパティ

実は、上記のコードでは少しばかりズルをしてしまい、値を変更できるクラスを作成してしまいました。オブジェクト指向のプログラミングでは、多くの場合、このように設計されるのですが……。

しかし、「テスト駆動開発入門」では、Kentはすぐにその問題に気づき、不変クラスに変更しているので、私も同じことをしましょう。

不変バージョンは以下の通りです。

type Dollar(amount:int) =
    member val Amount  = amount
    member this.Add add =
        Dollar (amount + add)
    member this.Times multiplier  =
        Dollar (amount * multiplier)
    static member Create amount  =
        Dollar amount

// 対話型テスト
let d1 = Dollar.Create 2
d1.Amount  // 2
let d2 = d1.Times 3
d2.Amount  // 6
let d3 = d2.Add 1
d3.Amount  // 7

不変コードの良い点は、セッターのテストの必要性をなくせることです。そのため、作成した2つのプロパティは無関係になりました。

正直言って、どちらにしてもかなり些細なことだったので、大した損失ではありません。

では、今度はどのような新しいプロパティを考案できるでしょうか？

Times メソッドを見てみましょう。どのようにテストすればよいでしょうか？どの戦略を使用できるでしょうか？

「異なるパス、同じ結果」の戦略が有効だと考えられます。ソートの場合と同様に、times演算を「内側」と「外側」の両方で行い、結果が同じになるかどうかを確認できます。

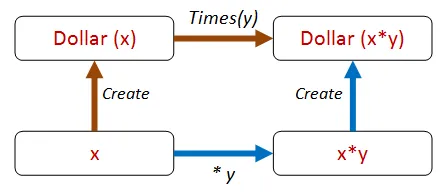
このプロパティをコードで表現すると、次のようになります。

let ``作成してから乗算した結果は、乗算してから作成した結果と同じである`` start multiplier =
    let d0 = Dollar.Create start
    let d1 = d0.Times(multiplier)
    let d2 = Dollar.Create (start * multiplier)
    d1 = d2

素晴らしい！動作するかどうか見てみましょう。

Check.Quick ``作成してから乗算した結果は、乗算してから作成した結果と同じである``
// 反証可能、1回のテスト後

おっと、動作しません。

なぜでしょうか？ Dollar が参照型であり、デフォルトでは等価比較されないことを忘れていたからです。

この間違いの結果、見落としていたかもしれないプロパティを発見しました。 忘れないうちに、それをコード化しましょう。

let ``同じ金額を持つドルは、等しい`` amount =
    let d1 = Dollar.Create amount
    let d2 = Dollar.Create amount
    d1 = d2

Check.Quick ``同じ金額を持つドルは、等しい``
// 反証可能、1回のテスト後

さて、コードを修正して、IEquatable などをサポートする必要がありますね。

そうやっても良いのですが、私はF#のレコード型に切り替えるので、等価比較は自動的にできます！

Dollarプロパティ - バージョン3

Dollar を書き直したものがこちらです。

type Dollar = {amount:int }
    with
    member this.Add add =
        {amount = this.amount + add }
    member this.Times multiplier  =
        {amount = this.amount * multiplier }
    static member Create amount  =
        {amount=amount}

そして、2つのプロパティが成立しました。

Check.Quick ``同じ金額を持つドルは、等しい``
// OK、100個のテストにパスしました。

Check.Quick ``作成してから乗算した結果は、乗算してから作成した結果と同じである``
// OK、100個のテストにパスしました。

このアプローチを異なるパスに拡張できます。たとえば、次のように、金額を抽出して直接比較できます。

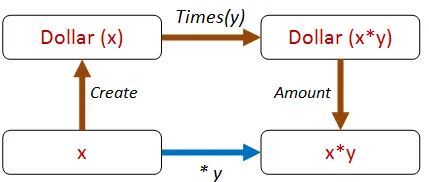
コードは以下のようになります。

let ``作成してから乗算し、値を取得した結果は、乗算した結果と同じである`` start multiplier =
    let d0 = Dollar.Create start
    let d1 = d0.Times(multiplier)
    let a1 = d1.amount
    let a2 = start * multiplier
    a1 = a2

Check.Quick ``作成してから乗算し、値を取得した結果は、乗算した結果と同じである``
// OK、100個のテストにパスしました。

また、Add もミックスに含めることができます。

たとえば、次のように、2つの異なるパスで Times の後に Add を実行できます。

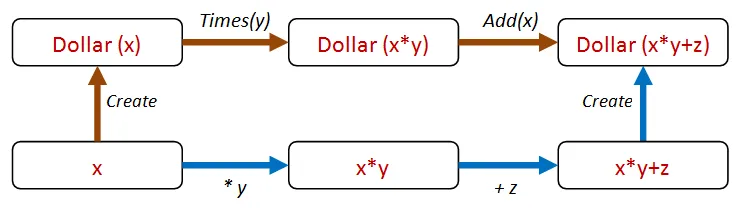
コードは以下の通りです。

let ``作成してから乗算し、加算した結果は、乗算し、加算してから作成した結果と同じである`` start multiplier adder =
    let d0 = Dollar.Create start
    let d1 = d0.Times(multiplier)
    let d2 = d1.Add(adder)
    let directAmount = (start * multiplier) + adder
    let d3 = Dollar.Create directAmount
    d2 = d3

Check.Quick ``作成してから乗算し、加算した結果は、乗算し、加算してから作成した結果と同じである``
// OK、100個のテストにパスしました。

このように、「異なるパス、同じ結果」アプローチは非常に実り多く、この方法で多くのパスを生成できます。

Dollarプロパティ - バージョン4

では、これで完成としてしまって良いのでしょうか？ いえ、まだです！

コードから嫌な臭いが漂ってきています。この (start * multiplier) + adder のようなコードは、ロジックの重複があり、変更に弱くなってしまいそうです。

これらのケースすべてに共通する部分を抽象化することはできるでしょうか？

考えてみると、ロジックは実際には次のとおりです。

• 金額を「内側」で何らかの方法で変換する。
• 金額を「外側」で同じ方法で変換する。
• 結果が同じであることを確認する。

しかし、これをテストするには、Dollar クラスが任意の変換をサポートする必要があります。それを Map と呼ぶことにしましょう。

これで、すべてのテストを次の1つのプロパティに減らすことができます。

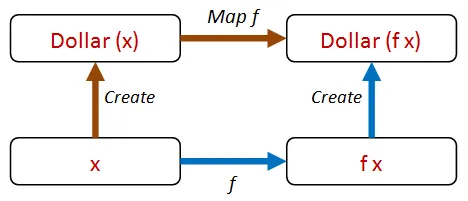
Dollar に Map メソッドを追加しましょう。また、Times と Add を Map で書き直すこともできます。

type Dollar = {amount:int }
    with
    member this.Map f =
        {amount = f this.amount}
    member this.Times multiplier =
        this.Map (fun a -> a * multiplier)
    member this.Add adder =
        this.Map (fun a -> a + adder)
    static member Create amount  =
        {amount=amount}

これで、プロパティのコードは以下のようになります。

let ``作成してからマップした結果は、マップしてから作成した結果と同じである`` start f =
    let d0 = Dollar.Create start
    let d1 = d0.Map f
    let d2 = Dollar.Create (f start)
    d1 = d2

しかし、どうやってテストすればいいのでしょうか？どのような関数を渡せばいいのでしょうか？

心配しないでください。FsCheckが対応しています。このような場合、FsCheckは実際にランダムな関数を生成してくれます。

試してみてください。動作します。

Check.Quick ``作成してからマップした結果は、マップしてから作成した結果と同じである``
// OK、100個のテストにパスしました。

新しい「map」プロパティは、「times」を使用した元のプロパティよりもはるかに一般的であるため、後者を安全に削除できます。

関数パラメータのログ出力

現状のプロパティにはちょっとした問題があります。FsCheckが生成している関数が何であるかを確認したい場合、Verboseモードは役に立ちません。

Check.Verbose ``作成してからマップした結果は、マップしてから作成した結果と同じである``

出力は以下のようになります。

0:
18
<fun:Invoke@3000>
1:
7
<fun:Invoke@3000>
-- etc
98:
47
<fun:Invoke@3000>
99:
36
<fun:Invoke@3000>
OK、100個のテストにパスしました。

関数の値が実際には何であったのかわかりません。

しかし、次のように、関数を特別な F ケースでラップすることで、FsCheckにさらに役立つ情報を表示するように指示できます。

let ``作成してからマップした結果は、マップしてから作成した結果と同じである２`` start (F (_,f)) =
    let d0 = Dollar.Create start
    let d1 = d0.Map f
    let d2 = Dollar.Create (f start)
    d1 = d2

そして、Verboseモードを使用すると…

Check.Verbose ``作成してからマップした結果は、マップしてから作成した結果と同じである２``

…使用された各関数の詳細なログが表示されます。

0:
0
{ 0->1 }
1:
0
{ 0->0 }
2:
2
{ 2->-2 }
-- etc
98:
-5
{ -5->-52 }
99:
10
{ 10->28 }
OK、100個のテストにパスしました。

各 { 2->-2 }、{ 10->28 } などは、その反復で使用された関数を表しています。

TDDとプロパティベースのテスト

プロパティベースのテスト（PBT）はTDDと両立できるものなのでしょうか？これはよくある質問なので、私の考えを簡単に説明させてください。

まず、TDDは具体的な例を扱いますが、PBTは普遍的なプロパティを扱います。

前回の投稿で述べたように、実例は設計への入り口として有用であり、ドキュメントの一種になり得ると考えています。 しかし、私の意見では、実例ベースのテストだけに頼るのは間違いです。

プロパティベースのアプローチは、実例ベースのテストに比べて、次のような多くの利点があります。

• プロパティベースのテストはより一般的なので、変更に対する弱さが軽減されます。
• プロパティベースのテストは、実例をいくつも並べるよりも、要件をより適切かつ簡潔に記述します。
• その結果、1つのプロパティベースのテストで、多くの実例ベースのテストを置き換えることができます。
• ランダムな入力を生成することで、プロパティベースのテストは、nullの処理、データの欠落、ゼロ除算、負の数など、見落としていた問題を明らかにすることがよくあります。
• プロパティベースのテストは、あなたに考えさせます。
• プロパティベースのテストは、あなたにクリーンな設計を強制します。

最後の2つのポイントが、私にとって最も重要です。プログラミングとは、コードを書くことではなく、要件を満たす設計を作成することです。

そのため、要件と何がうまくいかないかについて深く考えるのに役立つものはすべて、あなたの個人的なツールボックスの重要なツールになるはずです。

たとえば、ローマ数字のセクションでは、int を受け入れるのは悪い考えであること（コードが壊れる！）がわかりました。 とりあえず修正しましたが、実際にはドメインで PositiveInteger の概念をモデル化し、コードを単なる int ではなく、その型を使用するように変更する必要があります。 これは、PBTを使用することで、バグを見つけるだけでなく、ドメインモデルを実際に改善できることを示しています。

同様に、Dollarのシナリオで Map メソッドを導入したことで、テストが容易になっただけでなく、Dollarの「API」の有用性が実際に改善されました。

しかし、全体像に目を向けると、TDDとプロパティベースのテストは全く対立していません。 どちらも正しいプログラムを構築するという同じ目標を共有しており、どちらも実際にはコーディングよりも設計に関するものです（「テスト駆動開発」ではなく「テスト駆動設計」と考えてください）。

ついに終わり

これで、プロパティベースのテストに関する長い投稿は終わりです。

これで、独自のコードベースに持ち帰って適用できる、いくつかの有用なアプローチが得られたことを願っています。

次回は、実際の例と、ドメインに合ったカスタムジェネレーターを作成する方法について説明します。

この投稿で使用されているコードサンプルは、GitHubで入手できます。